题目内容
若函数f（x）满足方程af（x）+f（
）=ax，x∈R且x≠0，a为常数，且a≠±1，求f（x）的解析式．
| 1 |
| x |
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：由已知af（x）+f（
）=ax…①，以
代替x，得af（
）+f（x）=
…②；由①②组成方程组，求出f（x）的解析式．
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| a |
| x |
解答：
解：∵af（x）+f（
）=ax…①，且x≠0，
∴af（
）+f（x）=
…②；
∴①×a，得
a2f（x）+af（
）=a2x…③；
③-②，得
（a2-1）f（x）=a2x-
，
又∵a≠±1，∴a2-1≠0；
∴f（x）=
．
| 1 |
| x |
∴af（
| 1 |
| x |
| a |
| x |
∴①×a，得
a2f（x）+af（
| 1 |
| x |
③-②，得
（a2-1）f（x）=a2x-
| a |
| x |
又∵a≠±1，∴a2-1≠0；
∴f（x）=
| a2x2-a |
| a2x-x |
点评：本题考查了求函数定义域的问题，是基础题．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
下列四个命题：
①对于任意向量
、
，|
-
|≤|
|-|
|；
②向量
，
满足
•
=0，|
|=1，|
|=2，则|2
-
|=2
③对于非零向量
、
，
⊥
的充要条件是：|
+
|=|
-
|；
④在四边形ABCD中，
=2
，则该四边形为等腰梯形．
其中真命题是（ ）
①对于任意向量
| a |
| b |
| a |
| b |
| a |
| b |
②向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 2 |
③对于非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
④在四边形ABCD中，
| AD |
| BC |
其中真命题是（ ）
| A、②③ | B、①③ | C、③④ | D、①④ |
运行如图程序，如果输入x=
，则输出结果y为（ ）
| π |
| 6 |
A、2
| ||
| B、3 | ||
| C、2 | ||
D、
|
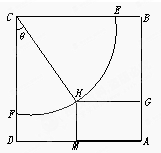某体育馆拟用运动场的边角地建一个矩形的健身室（如图所示），ABCD是一块边长为50m的正方形地皮，扇形CEF是运动场的一部分，其半径为40m，矩形AGHM就是拟建的健身室，其中G、M分别在AB和AD上，设矩形AGHM的面积为S，∠HCF=θ，请将S表示为θ的函数，并指出当点H在何处时，该健身室的面积最大，最大面积是多少？