题目内容
 如图,直三棱柱ABC-A1B1C1底面边长均为
如图,直三棱柱ABC-A1B1C1底面边长均为| 2 |
(Ⅰ)若D为A1C1的中点,求证:直线BC1∥平面AB1D;
(Ⅱ)设二面角A1-AB1-D的平面角为θ,
| A1D |
| A1C1 |
考点:用空间向量求平面间的夹角,直线与平面平行的判定,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(Ⅰ)连结A1B交AB1于点E,利用三角形中位线定理能证明BC1∥平面AB1D.
(Ⅱ)法一:过点D作DM⊥A1B1于M,则DM⊥平面ABB1A,过点M作MN⊥AB1于N,连结DN,则∠MND为二面角A1-AB1-D的平面角,由此能求出当λ=
时,能使tan θ=2.
(Ⅱ)法二:以AB的中点O为的点,建立空间直角坐标系,利用向量法能求出当λ=
时,能使tan θ=2.
(Ⅱ)法一:过点D作DM⊥A1B1于M,则DM⊥平面ABB1A,过点M作MN⊥AB1于N,连结DN,则∠MND为二面角A1-AB1-D的平面角,由此能求出当λ=
| 4 |
| 5 |
(Ⅱ)法二:以AB的中点O为的点,建立空间直角坐标系,利用向量法能求出当λ=
| 4 |
| 5 |
解答:
(Ⅰ)证明:连结A1B交AB1于点E,由E为A1B中点,
连结DE,∵D是A1C1中点,
∴DE∥BC1,
又DE?平面AB1D,BC1不包含于平面AB1D,
∴BC1∥平面AB1D.
(Ⅱ)解法一:过点D作DM⊥A1B1于M,则DM⊥平面ABB1A,
过点M作MN⊥AB1于N,连结DN,则∠MND为二面角A1-AB1-D的平面角.(6分)
过点A1作A1F⊥AB1于F,∵
=λ
(0<λ<1),
∴
=
=
,DM=A1Dsin 60°=
λ.(8分)
∵A1A=1,A1B1=
,则AB1=
,
∴A1F=
=
.(9分)
∵
=
=
=1-
,∴MN=
\b\lc\(\rc\)(\a\vs4\al\co1(1-
)).(10分)
∴tanθ=
=
=
,
由已知
=2,解得λ=

故当λ=
时,能使tan θ=2.(13分)
(Ⅱ)解法二:以AB的中点O为的点,如图所示建立空间直角坐标系,
则A(0,-
,0),A1(0,-
,1),B1(0,
,1),C1(-
,0,1),(6分)
=λ
(0<λ<1),则D(-
λ,0,1),(7分)
设
=(x,y,z)为平面AB1D的一个法向量,
由
•
=0,
•
=0,
得
=(1,
,
),(9分)
又
=(1,0,0)为平面AA1B1的一个法向量,
∴cos<
,
>=
=
,(10分)
∵tan θ=2,则cos θ=
,即cos<n1,n2>=
,
∴
=
.
化简,得5λ2+16λ-16=0,即(5λ-4)(λ+4)=0.
∵0<λ<1,则λ=
.
∴当λ=
时,能使tan θ=2.(13分)
连结DE,∵D是A1C1中点,
∴DE∥BC1,
又DE?平面AB1D,BC1不包含于平面AB1D,
∴BC1∥平面AB1D.
(Ⅱ)解法一:过点D作DM⊥A1B1于M,则DM⊥平面ABB1A,
过点M作MN⊥AB1于N,连结DN,则∠MND为二面角A1-AB1-D的平面角.(6分)
过点A1作A1F⊥AB1于F,∵
| A1D |
| A1C1 |
∴
| A1M |
| A1B1 |
| A1Dcos60° |
| A1C1 |
| λ |
| 2 |
| ||
| 2 |
∵A1A=1,A1B1=
| 2 |
| 3 |
∴A1F=
| A1A×A1B1 |
| AB1 |
| ||
| 3 |
∵
| MN |
| A1F |
| MB1 |
| A1B1 |
| A1B1-A1M |
| A1B1 |
| λ |
| 2 |
| ||
| 3 |
| λ |
| 2 |
∴tanθ=
| DM |
| MN |
| ||||||
|
| 3λ |
| 2-λ |
由已知
| 3λ |
| 2-λ |
| 4 |
| 5 |

故当λ=
| 4 |
| 5 |
(Ⅱ)解法二:以AB的中点O为的点,如图所示建立空间直角坐标系,
则A(0,-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| A1D |
| A1C1 |
| ||
| 2 |
设
| n1 |
由
| AD |
| n1 |
| B1D |
| n |
得
| n1 |
| ||
| λ-2 |
| ||
| 2-λ |
又
| n2 |
∴cos<
| n1 |
| n2 |
| 1 | ||||||||||
|
| 2-λ | ||
|
∵tan θ=2,则cos θ=
| ||
| 5 |
| ||
| 5 |
∴
| 2-λ | ||
|
| ||
| 5 |
化简,得5λ2+16λ-16=0,即(5λ-4)(λ+4)=0.
∵0<λ<1,则λ=
| 4 |
| 5 |
∴当λ=
| 4 |
| 5 |
点评:本题考查直线与平面平行的证明,考查满足条件的点是否存在的判断与求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
抛物线y=3x2的焦点坐标是( )
A、(0,
| ||
B、(0,-
| ||
C、(0,-
| ||
D、(0,
|
设离散型随机变量X的概率分布列如下表:
则p等于( )
| X | 1 | 2 | 3 | 4 | ||||||
| P |
| p |
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
 某农场有如图所示的六块田地,现有萝卜、玉米、油菜三类蔬菜可种.为有利于作物生长,要求每块田地种一类蔬菜,每类蔬菜种两块田地,每行、每列的蔬菜种类各不相同.则不同的种植方法数为( )
某农场有如图所示的六块田地,现有萝卜、玉米、油菜三类蔬菜可种.为有利于作物生长,要求每块田地种一类蔬菜,每类蔬菜种两块田地,每行、每列的蔬菜种类各不相同.则不同的种植方法数为( )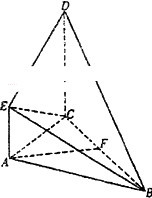 如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.
如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.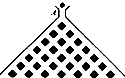 如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是