题目内容
若tanα=3，则cos2α等于（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点：二倍角的余弦
专题：三角函数的求值
分析：由同角三角函数的基本关系的应用，二倍角公式可得cos2α=
，再把tanα=3代入运算求得结果．
| 1-tan2α |
| 1+tan2α |
解答：
解：∵tanα=3，则cos2α=
=
=
=-
，
故选：D．
| cos2α-sin2α |
| cos2α+sin2α |
| 1-tan2α |
| 1+tan2α |
| 1-9 |
| 1+9 |
| 4 |
| 5 |
故选：D．
点评：本题主要考查同角三角函数的基本关系的应用，二倍角公式的应用，属于基础题．
练习册系列答案
相关题目
为了得到函数y=
（sin2x-cos2x）的图象，只要把函数y=sin2x的图象上所有的点（ ）
| ||
| 2 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
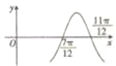
已知函数f（x）=cos（ωx+φ）（ω＞0，|φ|≤
）的图象如图所示，则φ等于（ ）
| π |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
已知定义在（0，+∞）上的单调函数f（x），对?x∈（0，+∞），都有f[f（x）-log3 x]=4，则函数g（x）=f（x-1）-f′（x-1）-3的零点所在区间是（ ）
| A、（1，2） | ||
| B、（2，3） | ||
C、（
| ||
D、（0，
|
某高中男子体育小组的50米跑成绩（单位：s）为6.4，6.5，7.0，6.8，7.1，7.3，6.9，7.4，7.5，如图是从这些成绩中搜索处小于6.8s的成绩的一个程序框图，则图中①②分别填上（ ）| A、r≥6.8，n＞9？ |
| B、r＜6.8，n＞9？ |
| C、r≥6.8，n≤9？ |
| D、r＜6.8，n≤9？ |
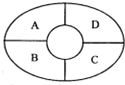如图某综艺节目现场设有A、B、C、D四个观众席，现有由3中不同颜色与2种不同款式组成的6中马甲安排给现场观众，要求每个观众席上的马甲相同，相邻观众席上的马甲的颜色与款式都不相同，则不同的安排方法种数为（ ）| A、72 | B、96 | C、36 | D、48 |
与30°角终边相同的角的集合是（ ）
| A、{θ|θ=30°+k•360°，k∈Z} |
| B、{θ|θ=30°+2k•360°，k∈Z} |
| C、{θ|θ=30°+k•180°，k∈Z} |
| D、{θ|θ=30°+k•90°，k∈Z} |