题目内容
已知复数z满足：iz=3+4i（i为虚数单位），则z的共轭复数在复平面内对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：复数代数形式的乘除运算,复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：把给出的等式两边同时乘以
，然后利用复数代数形式的除法运算化简求出z，则
的可求，答案可求．
| 1 |
| i |
. |
| z |
解答：
解：由iz=3+4i，得：
z=
=
=4-3i，
∴
=4+3i，
在复平面内对应的点的坐标为（4，3），位于第一象限．
故选：A．
z=
| 3+4i |
| i |
| (3+4i)(-i) |
| -i2 |
∴
. |
| z |
在复平面内对应的点的坐标为（4，3），位于第一象限．
故选：A．
点评：本题考查了复数代数形式的除法运算，考查了复数的代数表示法及其几何意义，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
为了得到函数y=
（sin2x-cos2x）的图象，只要把函数y=sin2x的图象上所有的点（ ）
| ||
| 2 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
等比数列{an}中，a3=16，a4=8，则a1=（ ）
| A、64 | B、32 | C、4 | D、2 |
将5名学生分到A，B，C三个宿舍，每个宿舍至少1人至多2人，其中学生甲不到A宿舍的不同分法有（ ）
| A、18种 | B、36种 |
| C、48种 | D、60种 |
集合A={x|x2＞1}，B={x|x+a≥0}，若∁UA⊆B，则实数a的取值范围是（ ）
| A、[-1，+∞） |
| B、[1，+∞） |
| C、（-∞，1] |
| D、（-∞，-1] |
已知函数f（x）=cos（ωx+φ）（ω＞0，|φ|≤
）的图象如图所示，则φ等于（ ）
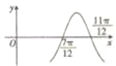
| π |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
已知定义在（0，+∞）上的单调函数f（x），对?x∈（0，+∞），都有f[f（x）-log3 x]=4，则函数g（x）=f（x-1）-f′（x-1）-3的零点所在区间是（ ）
| A、（1，2） | ||
| B、（2，3） | ||
C、（
| ||
D、（0，
|