题目内容
8.已知F1,F2分别是双曲线C:$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的左,右焦点,M是C上的一点,且|MF2|=10,则|MF1|=( )| A. | 10 | B. | 8 | C. | 4 | D. | 2 |
分析 利用双曲线的定义,转化求解即可.
解答 解:F1,F2分别是双曲线C:$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的左,右焦点,可得a=4,b=3,c=5,
M是C上的一点,且|MF2|=10,则|MF2|-|MF1|=2a=8,
解得|MF1|=2.
故选:D.
点评 本题考查双曲线的简单性质的应用,双曲线的定义,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
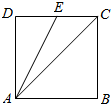
 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点,$PO=\sqrt{2},AB=2$.求证:
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点,$PO=\sqrt{2},AB=2$.求证: