题目内容
6.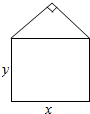 某单位用木料制作如图所示的框架,框架的下部是边长分别为x,y(单位:m)的矩形,上部是等腰直角三角形,要求框架围成的总面积为4m2,问x,y分别为多少时用料最省?并求最省用料.
某单位用木料制作如图所示的框架,框架的下部是边长分别为x,y(单位:m)的矩形,上部是等腰直角三角形,要求框架围成的总面积为4m2,问x,y分别为多少时用料最省?并求最省用料.
分析 通过设面积为S,利用S=xy+$\frac{{x}^{2}}{4}$=4可知y=$\frac{4}{x}$-$\frac{x}{4}$,进而化简可知c=$\frac{3+2\sqrt{2}}{2}$x+$\frac{8}{x}$,利用基本不等式计算即得结论.
解答 解:设面积为S,则S=xy+$\frac{{x}^{2}}{4}$=4,y=$\frac{4}{x}$-$\frac{x}{4}$,
∴c=2x+2y+$\sqrt{2}$x
=(2+$\sqrt{2}$)x+2($\frac{4}{x}$-$\frac{x}{4}$)
=$\frac{3+2\sqrt{2}}{2}$x+$\frac{8}{x}$
≥2$\sqrt{\frac{3+2\sqrt{2}}{2}x•\frac{8}{x}}$=4$\sqrt{2}$+4,
当且仅当$\frac{3+2\sqrt{2}}{2}$x=$\frac{8}{x}$即x=4$\sqrt{2}$-4、y=2时取等号,
于是当x=(4$\sqrt{2}$-4)米、y=2米时用料最省,为(4$\sqrt{2}$+4)米.
点评 本题考查函数模型的选择与应用,考查基本不等式,注意解题方法的积累,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
14.已知0<θ≤$\frac{π}{2}$,则方程x2+y2•sinθ=1表示的平面图形是( )
| A. | 焦点在x轴的椭圆 | B. | 焦点在y轴的椭圆 | ||
| C. | 圆或焦点在x轴的椭圆 | D. | 圆或焦点在y轴的椭圆 |
15.在平面直角坐标系中,直线y=2x+1的图象不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |