题目内容
7.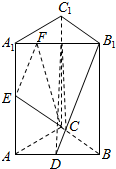 如图,在三棱柱ABC-A1B1C1中,D、E分别是AB、AA1的中点,AA1⊥平面ABC,AB⊥AC,AA1=4,AB=AC=2,且$\overrightarrow{{A}_{1}F}$=$\frac{1}{4}$$\overrightarrow{{A}_{1}{B}_{1}}$.
如图,在三棱柱ABC-A1B1C1中,D、E分别是AB、AA1的中点,AA1⊥平面ABC,AB⊥AC,AA1=4,AB=AC=2,且$\overrightarrow{{A}_{1}F}$=$\frac{1}{4}$$\overrightarrow{{A}_{1}{B}_{1}}$.(1)证明:B1D∥平面CEF;
(2)求异面直线CE与C1D所成角的余弦值.
分析 (1)取A1B1的中点G,连结AG,推导出四边形ADB1G为平行四边形,由此能证明B1D∥平面CEF.
(2)分别以AC、AB、AA1为x,y,z轴,建立空间直角坐标系,利用向量法能求出异面直线CE与C1D所成角的余弦值.
解答 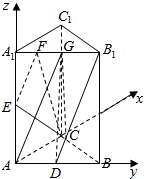 证明:(1)取A1B1的中点G,连结AG,
证明:(1)取A1B1的中点G,连结AG,
∵$\overrightarrow{{A}_{1}F}=\frac{1}{4}\overrightarrow{{A}_{1}{B}_{1}}$,∴F为A1A的中点,又E为AA1中点,∴EF∥AG,
∵A1B1$\underset{∥}{=}$AB,D为AB中点,∴$AD\underset{∥}{=}{B}_{1}G$,
∴四边形ADB1G为平行四边形,
∴AG∥B1D,∴EF∥B1D,又EF?平面CEF,B1D?平面CEF,
∴B1D∥平面CEF.
解:(2)分别以AC、AB、AA1为x,y,z轴,建立空间直角坐标系,
则C1(2,0,4),C(2,0,0),D(0,1,0),E(0,0,2),
∴$\overrightarrow{{C}_{1}D}$=(-2,1,-4),$\overrightarrow{CE}$=(-2,0,2),
∴cos<$\overrightarrow{{C}_{1}D}$,$\overrightarrow{CE}$>=$\frac{\overrightarrow{{C}_{1}D}•\overrightarrow{CE}}{|\overrightarrow{{C}_{1}D}||\overrightarrow{CE}|}$=$\frac{4-8}{\sqrt{21}×2\sqrt{2}}$=-$\frac{\sqrt{42}}{21}$,
∴异面直线CE与C1D所成角的余弦值为$\frac{\sqrt{42}}{21}$.
点评 本题考查线面平行的证明,考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

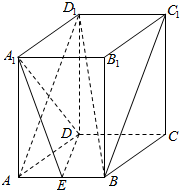 长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点.
长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点.