题目内容
2.已知tanα=2,并且α为第三象限的角,那么cosα=( )| A. | -$\frac{2\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
分析 首先,利用1+tan2α=$\frac{1}{co{s}^{2}α}$,再根据α为第三象限的角得到cosα.
解答 解:∵tanα=2,
1+tan2α=$\frac{1}{co{s}^{2}α}$,
∴cos2α=$\frac{1}{5}$
∵α是第三象限角,
∴cosα=-$\frac{\sqrt{5}}{5}$,
故选:C
点评 本题重点考查了同角三角函数基本关系式及其灵活运用,注意角度的取值范围问题,防止增根的产生

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.在△ABC中,点M在边BC上,且2$\overrightarrow{BM}$=3$\overrightarrow{MC}$,E在边AC上,且$\overrightarrow{EC}$=3$\overrightarrow{AE}$,则向量$\overrightarrow{EM}$-$\overrightarrow{AB}$=( )
| A. | $\frac{7}{20}$$\overrightarrow{AC}$-$\frac{3}{5}$$\overrightarrow{AB}$ | B. | $\frac{7}{20}$$\overrightarrow{AC}$+$\frac{2}{5}$$\overrightarrow{AB}$ | C. | $\frac{2}{5}$$\overrightarrow{AC}$-$\frac{3}{5}$$\overrightarrow{AB}$ | D. | $\frac{1}{3}$$\overrightarrow{AC}$+$\frac{1}{5}$$\overrightarrow{AB}$ |
14.已知0<θ≤$\frac{π}{2}$,则方程x2+y2•sinθ=1表示的平面图形是( )
| A. | 焦点在x轴的椭圆 | B. | 焦点在y轴的椭圆 | ||
| C. | 圆或焦点在x轴的椭圆 | D. | 圆或焦点在y轴的椭圆 |
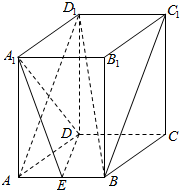 长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点.
长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点. 如图,已知圆柱的高为4,AA1,BB1,CC1是圆柱的三条母线,AB是底面圆O的直径,AC=3,AB=5.
如图,已知圆柱的高为4,AA1,BB1,CC1是圆柱的三条母线,AB是底面圆O的直径,AC=3,AB=5.