题目内容
随机向边长为5,5,6的三角形中投一点P,则点P到三个顶点的距离都不小于1的概率是 .
考点:几何概型
专题:计算题,作图题,概率与统计
分析:本题符合几何概型,由题意作图,求面积比即可.
解答:
解:本题符合几何概型,由题意作图如下,

则点P应落在黑色阴影部分,
S△=
×6×
=12,
三个小扇形可合并成一个半圆,故其面积S=
π,
故点P到三个顶点的距离都不小于1的概率P=
=
.
故答案为:
.

则点P应落在黑色阴影部分,
S△=
| 1 |
| 2 |
| 52-32 |
三个小扇形可合并成一个半圆,故其面积S=
| 1 |
| 2 |
故点P到三个顶点的距离都不小于1的概率P=
12-
| ||
| 12 |
| 24-π |
| 24 |
故答案为:
| 24-π |
| 24 |
点评:本题考查了几何概型概率的求法,属于基础题.

练习册系列答案
相关题目
已知平面内一点P及△ABC,若
+
+
=
,则点P与△ABC的位置关系是( )
| PA |
| PB |
| PC |
| AB |
| A、点P在线段AB上 |
| B、点P在线段BC上 |
| C、点P在线段AC上 |
| D、点p在△ABC外部 |
设m,n表示不同直线,α,β表示不同平面,则下列命题中正确的是( )
| A、若m∥α,m∥n,则n∥α |
| B、若m?α,n?β,n∥α,则α∥β |
| C、若α∥β,m∥α,m∥n,则n∥β |
| D、若α∥β,m∥α,n∥m,n?β,则n∥β |
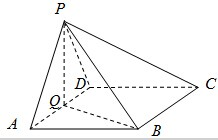 在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,若PA=PD.
在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,若PA=PD.