题目内容
已知直角三角形ABE,AB⊥BE,AB=2BE=4,C,D分别是AB,AE上的中点,且CD∥BE,将△ACD沿CD折起到位置A1CD,使平面A1CD与平面BCD所成的二面角A1-CD-B的大小为θ,.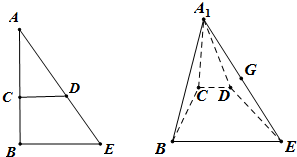
(1)若θ=
,求直线A1E与平面BCD所成的角的正切值;
(2)已知G为A1E的中点,若BG⊥A1D,求cosθ的取值.

(1)若θ=
| π |
| 3 |
(2)已知G为A1E的中点,若BG⊥A1D,求cosθ的取值.
考点:直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(1)首先利用折叠前的相关量利用勾股定理,求出对应的线段长,利用θ=
,最为突破口,求出相对应的结果.
(2)采用转化法取DE中点H,连接GH,BH,因为G是A1E中点,所以GH∥A1D进一步求出,BG⊥GH和
A1C=CB=2,BE=2,A1D=DE=
,所以GH=
,EH=
最后利用三角形的关系解得:cos∠BEH=
,利用余弦定理得:BH=
,所以利用勾股定理得BG=
,因为BE⊥面A1BC,所以∠A1BE=90°,
A1E=2BG=2
,A1B=2,A1C=A1B=BC=2最后求得结果.
| π |
| 3 |
(2)采用转化法取DE中点H,连接GH,BH,因为G是A1E中点,所以GH∥A1D进一步求出,BG⊥GH和
A1C=CB=2,BE=2,A1D=DE=
| 5 |
| ||
| 2 |
| ||
| 2 |
| ||
| 5 |
| ||
| 2 |
| 2 |
A1E=2BG=2
| 2 |
解答:
解:(1)直角三角形ABE,AB⊥BE,AB=2BE=4,C,D分别是AB,AE上的中点,且CD∥BE,将△ACD沿CD折起到位置,使平面A1CD与平面BCD所成的二面角A1-CD-B的大小为θ,
当θ=
时,
求得:△A1BC为等边三角形
取BC得中点F,
BF=CF=1
进一步利用勾股定理解得:A1F=
FE=
所以:直线A1E与平面BCD所成的角的正切值:
tanθ=
=
(2)取DE中点H,连接GH,BH
因为G是A1E中点
所以GH∥A1D
因为BG⊥A1D
所以BG⊥GH
所以A1C=CB=2,BE=2,A1D=DE=
所以GH=
,EH=
cos∠BEH=
利用余弦定理得:
BH=
所以勾股定理得BG=
因为BE⊥面A1BC
所以∠A1BE=90°
A1E=2BG=2
,A1B=2,A1C=A1B=BC=2
所以cosθ=cos60°=

当θ=
| π |
| 3 |
求得:△A1BC为等边三角形
取BC得中点F,
BF=CF=1
进一步利用勾股定理解得:A1F=
| 3 |
FE=
| 17 |
所以:直线A1E与平面BCD所成的角的正切值:
tanθ=
| A1F |
| EF |
3
| ||
| 17 |
(2)取DE中点H,连接GH,BH
因为G是A1E中点
所以GH∥A1D
因为BG⊥A1D
所以BG⊥GH
所以A1C=CB=2,BE=2,A1D=DE=
| 5 |
所以GH=
| ||
| 2 |
| ||
| 2 |
cos∠BEH=
| ||
| 5 |
利用余弦定理得:
BH=
| ||
| 2 |
所以勾股定理得BG=
| 2 |
因为BE⊥面A1BC
所以∠A1BE=90°
A1E=2BG=2
| 2 |
所以cosθ=cos60°=
| 1 |
| 2 |

点评:本题考查的知识要点:线面的夹角问题的应用,面面夹角的应用及相关的运算问题.属于中等难度题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列几个图形中,可以表示函数关系y=f(x)的一个图是( )
A、 |
B、 |
C、 |
D、 |
已知平面内一点P及△ABC,若
+
+
=
,则点P与△ABC的位置关系是( )
| PA |
| PB |
| PC |
| AB |
| A、点P在线段AB上 |
| B、点P在线段BC上 |
| C、点P在线段AC上 |
| D、点p在△ABC外部 |
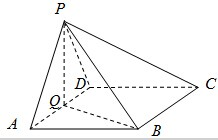 在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,若PA=PD.
在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,若PA=PD.