题目内容
18.已知关于x的方程$\frac{{x}^{2}+2}{x(lnx+k)+2k}$=1在x∈[$\frac{1}{2}$,+∞]上有两个不相等的实数根,则实数k的取值范围为(1,$\frac{9+2ln2}{10}$].分析 化简方程得x2-xlnx+2=k(x+2),判断左侧函数的单调性,作出函数图象,根据图象交点个数判断k的范围.
解答 解:由$\frac{{x}^{2}+2}{x(lnx+k)+2k}=1$得x2-xlnx+2=k(x+2),
令f(x)=x2-xlnx+2(x$≥\frac{1}{2}$),则f′(x)=2x-lnx-1,
f″(x)=2-$\frac{1}{x}$,∵x$≥\frac{1}{2}$,∴f″(x)≥0,
∴f′(x)在[$\frac{1}{2}$,+∞)上单调递增,∴f′(x)≥f′($\frac{1}{2}$)=-ln$\frac{1}{2}$>0,
∴f(x)在[$\frac{1}{2}$,+∞)上是增函数,
作出f(x)在[$\frac{1}{2}$,+∞)上的函数图象如图所示: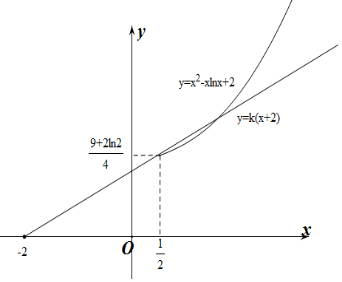
当直线y=k(x+2)经过点($\frac{1}{2}$,$\frac{9+2ln2}{4}$)时,k=$\frac{9+2ln2}{10}$,
当直线y=k(x+2)与y=f(x)相切时,设切点为(x0,y0),
则$\left\{\begin{array}{l}{{y}_{0}=k({x}_{0}+2)}\\{{y}_{0}={{x}_{0}}^{2}-{x}_{0}ln{x}_{0}+2}\\{2{x}_{0}-ln{x}_{0}-1=k}\end{array}\right.$,解得x0=1,y0=3,k=1.
∵方程$\frac{{x}^{2}+2}{x(lnx+k)+2k}$=1在x∈[$\frac{1}{2}$,+∞)上有两个不相等的实数根,
∴直线y=k(x+2)与y=f(x)的图象有两个交点,
∴1<k≤$\frac{9+2ln2}{10}$.
故答案为(1,$\frac{9+2ln2}{10}$].
点评 本题考查了根的个数与函数图象的关系,函数单调性的判断,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | [-2,1)∪[4,7) | B. | (-2,1]∪[4,7] | C. | (-2,1]∪(4,7) | D. | (-2,1]∪[4,7) |

| A. | -2 | B. | 1 | C. | 2 | D. | 4 |
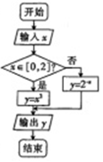 如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )
如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )| A. | [-3,-2] | B. | [-3,-2)∪{2} | C. | [-3,2] | D. | [-3,-2]∪{2} |
| A. | 120 | B. | 119 | C. | 114 | D. | 110 |
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{8}$ | D. | $\frac{{\sqrt{2}}}{16}$ |
| A. | P∪Q=P | B. | P∩Q?Q | C. | P∪Q=Q | D. | P∩Q⊆P |
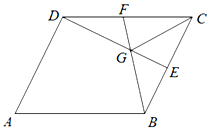 如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC、DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$.
如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC、DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$. 将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式:
将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式: