题目内容
7.在平面直角坐标系xOy中,已知双曲线C1:2x2-y2=1,过C1的左顶点引C1的一条渐进线的平行线,则该直线与另一条渐进线及x轴围成的三角形的面积( )| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{8}$ | D. | $\frac{{\sqrt{2}}}{16}$ |
分析 双曲线C1:左顶点A(-$\frac{\sqrt{2}}{2}$,0),过点A与渐近线y=$\sqrt{2}$x平行的直线方程为y=$\sqrt{2}$x+1,由此能求出该直线与另一条渐近线及x轴围成的三角形的面积.
解答 解:双曲线C1:2x2-y2=1,即$\frac{{x}^{2}}{\frac{1}{2}}$-y2=1左顶点A(-$\frac{\sqrt{2}}{2}$,0),
渐近线方程y=±$\sqrt{2}$x,
过点A与渐近线y=$\sqrt{2}$平行的直线方程为y=$\sqrt{2}$(x+$\frac{\sqrt{2}}{2}$),
即y=$\sqrt{2}$x+1,
解方程组$\left\{\begin{array}{l}{y=-\sqrt{2}x}\\{y=\sqrt{2}x+1}\end{array}\right.$,得x=-$\frac{\sqrt{2}}{4}$,y=$\frac{1}{2}$
∴该直线与另一条渐近线及x轴围成的三角形的面积:S=$\frac{1}{2}$|OA|•|y|=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$×$\frac{1}{2}$=$\frac{\sqrt{2}}{8}$,
故选:C
点评 本题考查三角形面积的求法,解题时要认真审题,注意函数与方程思想的合理运用,属于基础题.

练习册系列答案
相关题目
17.设D=$\sqrt{{{({x-a})}^2}+{{({lnx-\frac{a^2}{4}})}^2}}+\frac{a^2}{4}$+1.(a∈R),则D的最小值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
15.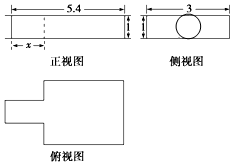 中国古代数学著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其几何体体积为13.5(立方寸),则图中x的为( )
中国古代数学著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其几何体体积为13.5(立方寸),则图中x的为( )
 中国古代数学著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其几何体体积为13.5(立方寸),则图中x的为( )
中国古代数学著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其几何体体积为13.5(立方寸),则图中x的为( )| A. | 2.4 | B. | 1.8 | C. | 1.6 | D. | 1.2 |
2.如图,给出的是$1+\frac{1}{3}+\frac{1}{5}+…+\frac{1}{99}$的值的一个程序框图,判断框内应填入的条件是( )
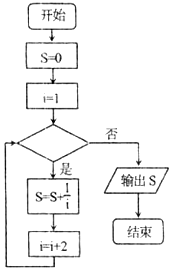

| A. | i<99 | B. | i≤99 | C. | i>99 | D. | i≥99 |
12.若直线ax-by+2=0 (a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为( )
| A. | $\frac{3}{2}$+$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{2}$+2$\sqrt{2}$ |
19.已知A,B是单位圆O上的两个动点,|AB|=$\sqrt{2}$,$\overrightarrow{OC}$=2$\overrightarrow{OA}$-$\overrightarrow{OB}$.若M是线段AB的中点,则$\overrightarrow{OC}$•$\overrightarrow{OM}$的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
6.已知$a=\frac{1}{2}$,$b={3^{\frac{1}{2}}}$,c=log32,则( )
| A. | b>a>c | B. | c>b>a | C. | b>c>a | D. | a>b>c |
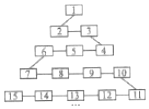 一般吧数字出现的规律满足如图的模型称为蛇形模型:数字1出现在第1行,数字2,3出现在第2行;数字6,5,4(从左到右)出现在第3行;数字7,8,9,10出现在第4行,以此类推,第21行从左到右的第4个数字应是228.
一般吧数字出现的规律满足如图的模型称为蛇形模型:数字1出现在第1行,数字2,3出现在第2行;数字6,5,4(从左到右)出现在第3行;数字7,8,9,10出现在第4行,以此类推,第21行从左到右的第4个数字应是228.