题目内容
8.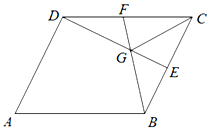 如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC、DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$.
如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC、DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$.(1)试用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{AG}$;
(2)求$\overrightarrow{BF}•\overrightarrow{AG}$的值.
分析 (1)利用向量的加法以及三角形的重心坐标关系推出结果即可.
(2)表示出向量,利用数量积化简求解即可.
解答 解:(1)由题意若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$.
推出:$\overrightarrow{AE}$=$\overrightarrow{AB}$+$\overrightarrow{BE}$=$\overrightarrow{a}$$+\frac{1}{2}\overrightarrow{b}$,
$\overrightarrow{BF}$=$\overrightarrow{BC}+\overrightarrow{CF}$=-$\frac{1}{2}$$\overrightarrow{a}+\overrightarrow{b}$,
E、F分别是BC,DC的中点,G为 BF、DE的交点,
所以G为△BCD的重心,∴$\overrightarrow{BG}=\frac{2}{3}\overrightarrow{BF}$,
$\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{BG}$=$\overrightarrow{a}+\frac{2}{3}(-\frac{1}{2}\overrightarrow{a}+\overrightarrow{b})$=$\frac{2}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}$.…(3分)
(2)若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$.
$\overrightarrow{BF}$=$\overrightarrow{BC}+\overrightarrow{CF}$=-$\frac{1}{2}$$\overrightarrow{a}+\overrightarrow{b}$,
$\overrightarrow{AG}$=$\frac{2}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}$.
∴$\overrightarrow{BF}•\overrightarrow{AG}$=$(-\frac{1}{2}\overrightarrow{a}+\overrightarrow{b})(\frac{2}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b})$
=$-\frac{1}{3}{\overrightarrow{a}}^{2}+\frac{1}{3}\overrightarrow{a}•\overrightarrow{b}+\frac{2}{3}{\overrightarrow{b}}^{2}$
=$-\frac{1}{3}$$|\overrightarrow{a}{|}^{2}+\frac{1}{3}|\overrightarrow{a}||\overrightarrow{b}|cos60°+\frac{2}{3}|\overrightarrow{b}{|}^{2}$
=$-\frac{4}{3}+\frac{2}{3}+\frac{8}{3}$=2.…(6分)
点评 本题考查向量的数量积的应用,向量在三角形中的应用,考查计算能力.

 阅读快车系列答案
阅读快车系列答案| A. | ($\frac{1}{4}$,$\frac{5}{4}$]∪($\frac{7}{4}$,+∞) | B. | ($\frac{1}{4}$,$\frac{7}{4}$) | C. | (-∞,$\frac{1}{4}$]∪[$\frac{5}{4}$,+∞) | D. | ($\frac{1}{4}$,$\frac{5}{4}$]∪[$\frac{7}{4}$,+∞) |
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
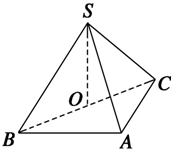 如图所示,在三棱锥S-ABC中,SO⊥平面ABC,侧面SAB与SAC均为等边三角形,∠BAC=90°,O为BC的中点,求二面角A-SC-B的余弦值.
如图所示,在三棱锥S-ABC中,SO⊥平面ABC,侧面SAB与SAC均为等边三角形,∠BAC=90°,O为BC的中点,求二面角A-SC-B的余弦值.