题目内容
9.不等式3≤|5-2x|<9的解集为( )| A. | [-2,1)∪[4,7) | B. | (-2,1]∪[4,7] | C. | (-2,1]∪(4,7) | D. | (-2,1]∪[4,7) |
分析 由不等式可得3≤2x-5<9 或-9<2x-5≤-3,由此求得不等式的解集.
解答 解:由不等式3≤|5-2x|<9 可得3≤2x-5<9 或-9<2x-5≤-3,
解得 4≤x<7,或-2<x≤1,
不等式3≤|5-2x|<9的解集为:{x|4≤x<7,或-2<x≤1},
故选:D.
点评 题主要考查绝对值不等式的解法,体现了等价转化的数学思想,属于中档题.

练习册系列答案
相关题目
20.已知函数f(x)=$\left\{\begin{array}{l}{(lnx)^{2}+alnx+b,x>0}\\{{e}^{x}+\frac{1}{4},x≤0}\end{array}\right.$,且f(e)=f(1),f(e2)=f(0)+$\frac{11}{4}$,则函数f(x)的值域为( )
| A. | ($\frac{1}{4}$,$\frac{5}{4}$]∪($\frac{7}{4}$,+∞) | B. | ($\frac{1}{4}$,$\frac{7}{4}$) | C. | (-∞,$\frac{1}{4}$]∪[$\frac{5}{4}$,+∞) | D. | ($\frac{1}{4}$,$\frac{5}{4}$]∪[$\frac{7}{4}$,+∞) |
17.设D=$\sqrt{{{({x-a})}^2}+{{({lnx-\frac{a^2}{4}})}^2}}+\frac{a^2}{4}$+1.(a∈R),则D的最小值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
4.空间四边形ABCD的四个顶点都在同一球面上,E、F分别是AB、CD的中点,且EF⊥AB,EF⊥CD,若AB=8,CD=EF=4,则该球的半径等于( )
| A. | $\frac{{65\sqrt{2}}}{16}$ | B. | $\frac{{65\sqrt{2}}}{8}$ | C. | $\frac{{\sqrt{65}}}{2}$ | D. | $\sqrt{65}$ |
14.上面图给出的是计算1+2+4+…+22017的值的一个程序框图,则其中判断框内应填入的是( ) 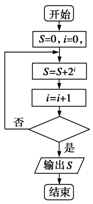

| A. | i=2017? | B. | i≥2017? | C. | i≥2018? | D. | i≤2018? |