题目内容
在平面xOy中,不等式x2+y2≤4确定的平面区域为U,不等式组
确定的平面区域为V.
(Ⅰ)在区域U中任取一个点,若所取的点落在区域V中,称试验成功,求实验成功的概率;
(Ⅱ)定义横、纵坐标为整数的点为“整点”,在区域U中任取1个“整点”,求这些“整点”恰好落在区域V中的概率.
|
(Ⅰ)在区域U中任取一个点,若所取的点落在区域V中,称试验成功,求实验成功的概率;
(Ⅱ)定义横、纵坐标为整数的点为“整点”,在区域U中任取1个“整点”,求这些“整点”恰好落在区域V中的概率.
考点:几何概型,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)根据几何概型的概率公式求出相应的面积,即可得到结论,
(Ⅱ)根据古典概型的概率公式分别求出对应区域内的“整点”个数,即可得到结论.
(Ⅱ)根据古典概型的概率公式分别求出对应区域内的“整点”个数,即可得到结论.
解答:
解:(1)作出不等式组对应的平面区域如图: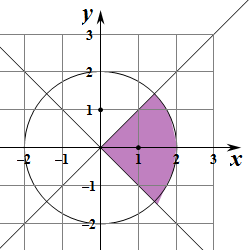
则平面区域为V对应的面积为
×π×22=π,
则实验成功的概率为
=
.
(2)区域U内的“整点”共有13个,平面区域为V内的“整点”个数为3个,
则由古典概型的概率公式可知在区域U中任取1个“整点”,求这些“整点”恰好落在区域V中的概率为
.

则平面区域为V对应的面积为
| 1 |
| 4 |
则实验成功的概率为
| π |
| π×22 |
| 1 |
| 4 |
(2)区域U内的“整点”共有13个,平面区域为V内的“整点”个数为3个,
则由古典概型的概率公式可知在区域U中任取1个“整点”,求这些“整点”恰好落在区域V中的概率为
| 5 |
| 13 |
点评:本题主要考查概率的计算,利用几何概型和古典概型的概率公式是解决本题的关键,利用数形结合是解决本题的突破.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
抛物线y=x2-2mx+m+2的顶点在第三象限,试确定m的取值范围是( )
| A、m<-1或m>2 |
| B、m<0或m>-1 |
| C、-1<m<0 |
| D、m<-1 |