题目内容
10.已知函数f(x)=x2.(1)若曲线f(x)的一条切线的斜率是2,求切点的坐标;
(2)求在点(-1,f(-1))处的切线方程;
(3)求过点(1,-2)处的切线方程.
分析 (1)设切点坐标,根据导数的几何意义可知切线的斜率为f′(t)=2,从而可求出切点坐标;
(2)先求出k=f′(-1)的值,得到切线的斜率,再求出切点坐标,最后根据点斜式求出直线方程即可.
(3)求出原函数的导函数,设出切点坐标,表示出切线方程,将(1,-2)代入切线方程,求出切点坐标,从而求出切线方程即可.
解答 解:(1)设切点坐标为(t,t2),
根据导数的几何意义可知切线的斜率为f′(t)=2t=2,解得t=1,
∴切点坐标为(1,1);
(2)∵f′(x)=2x,
∴k=f′(-1)=-2,
而f(-1)=1,则切点为(-1,1),
∴切线方程为y-1=-2[x-(-1)],即2x+y+1=0.
(3)由f(x)=x2,得f′(x)=2x,
设切点坐标是(a,a2),
则f′(a)=2a,
故切线方程是:y-a2=2a(x-a),
将(1,-2)代入切线方程得:
-2-a2=2a(1-a),解得:a=1±$\sqrt{3}$,
故切线方程是:y=2(1+$\sqrt{3}$)x-(4+2$\sqrt{3}$)
或y=2(1-$\sqrt{3}$)x-(4-2$\sqrt{3}$).
点评 本题主要考查了利用导数研究曲线上某点切线方程,以及导数的几何意义,同时考查了运算求解的能力,属于中档题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
12.在△ABC中,A=30°,AB=2,且△ABC的面积为$\sqrt{3}$,则△ABC外接圆的半径为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4\sqrt{3}}{3}$ | C. | 2 | D. | 4 |
15.已知f(x)=cos(ωx+φ)(ω>0),f'(x)是f(x)的导函数,若f(α)=0,f'(α)>0,且f(x)在[α,π+α)上没有最小值,则ω的取值范围是( )
| A. | $(0,\frac{1}{2})$ | B. | $(0,\frac{3}{2}]$ | C. | $(1,\frac{3}{2}]$ | D. | (1,+∞) |
19.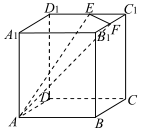 如图所示,在棱长为 6的正方体ABCD-A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,过A,E,F三点作该正方体的截面,则截面的周长为( )
如图所示,在棱长为 6的正方体ABCD-A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,过A,E,F三点作该正方体的截面,则截面的周长为( )
 如图所示,在棱长为 6的正方体ABCD-A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,过A,E,F三点作该正方体的截面,则截面的周长为( )
如图所示,在棱长为 6的正方体ABCD-A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,过A,E,F三点作该正方体的截面,则截面的周长为( )| A. | $18+3\sqrt{2}$ | B. | $6\sqrt{13}+3\sqrt{2}$ | C. | $6\sqrt{5}+9\sqrt{2}$ | D. | $10+3\sqrt{2}+4\sqrt{10}$ |