题目内容

10．已知cos2α=sinα，则$\frac{1}{sinα}+{cos^4}α$=2．

分析 利用同角三角函数的基本关系，求得sinα的值，可得要求式子的值．

解答 解：cos2α=sinα=1-sin2α，∴sinα=$\frac{-1+\sqrt{5}}{2}$，或sinα=$\frac{-1-\sqrt{5}}{2}$（舍去），
则$\frac{1}{sinα}+{cos^4}α$=$\frac{1}{sinα}$+sin2α=$\frac{2}{-1+\sqrt{5}}$+${（\frac{-1+\sqrt{5}}{2}）}^{2}$=2，
故答案为：2．

点评 本题主要考查同角三角函数的基本关系的应用，属于基础题．

练习册系列答案
相关题目
20．椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{6}}{3}$，各个顶点围成的菱形面积为2$\sqrt{3}$．
（1）求C的方程；
（2）过右顶点A的直线l交椭圆C于A，B两点．
①若|AB|=$\frac{4\sqrt{15}}{7}$，求l的方程；
②点P（0，y0）在线段AB的垂直平分线上，且$\overrightarrow{PA}$$•\overrightarrow{PB}$=3，求y0．
1．若${（1+x）^6}{（1-2x）^5}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_{11}}{x^{11}}$，求
（1）a1+a2+a3+…+a11；
（2）a0+a2+a4+…+a10．
18．复数$z=\frac{2+mi}{1+i}（m∈R）$是实数，则m=（　　）
A．-2B．-1C．1D．2
5．设${\vec e_1}，{\vec e_2}$为单位向量，非零向量$\vec b=x{\vec e_1}+y{\vec e_2}，x，y∈R$．若${\vec e_1}，{\vec e_2}$的夹角为$\frac{π}{6}$，则$\frac{|x|}{{|{\vec b}|}}$的最大值等于（　　）
A．4B．3C．2D．1
3．已知函数f（x）=cosx（2sinx+mcosx）的图象经过点P（π，-2$\sqrt{3}$）．
（1）求m的值以及f（$\frac{π}{6}$）；
（2）函数f（x）的图象向右平移$\frac{π}{6}$后得到函数g（x）的图象，求g（x）在[0，$\frac{π}{2}$]上的值域．
10．已知函数f（x）=x2．
（1）若曲线f（x）的一条切线的斜率是2，求切点的坐标；
（2）求在点（-1，f（-1））处的切线方程；
（3）求过点（1，-2）处的切线方程．
7．一个几何体的三视图如图所示，则该几何体的体积为（　　）
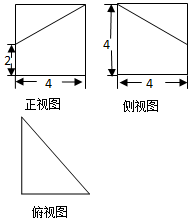
A．$\frac{32}{3}$B．$\frac{50}{3}$C．$\frac{64}{3}$D．$\frac{80}{3}$
8．$f（x）=a{e^x}lnx+\frac{{b{e^{x-1}}}}{x}$，曲线y=f（x）在点（1，f（1）处切线为y=e（x-1）+2，则a+b=3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网