题目内容
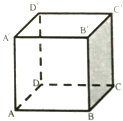
如图是正方体ABCD-A′B′C′D′中，异面直线A′D与CD′所成的角是（ ）
| A、30° | B、45° |
| C、60° | D、90° |
考点：异面直线及其所成的角
专题：空间角
分析：首先通过做平行线把异面直线所成的角转化为平面直线所成的角，进一步通过解三角形知识得到结果．
解答：
解：在正方体ABCD-A′B′C′D′中，连结CB′，B′D′
设正方体的边长为1，
在△CB′D′中，CD′=CB′=B′D′=
所以：△CB′D′为等边三角形
∠B′CD′=60°
即：异面直线A′D与CD′所成的角为：60°
故选：C
设正方体的边长为1，
在△CB′D′中，CD′=CB′=B′D′=
| 2 |
所以：△CB′D′为等边三角形
∠B′CD′=60°
即：异面直线A′D与CD′所成的角为：60°
故选：C
点评：本题考查的知识要点：空间问题向平面问题的转化，异面直线的夹角问题．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）的导函数图象如图所示，若△ABC是以角C为钝角的钝角三角形，则一定成立的是（ ）
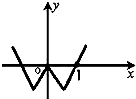
| A、f（sinA）＞f（cosB） |
| B、f（sinA）＜f（cosB） |
| C、f（sinA）＞f（sinB） |
| D、f（cosA）＜f（cosB） |
若变量x，y满足约束条件
，则z=2x+y的最大值为（ ）
|
| A、1 | B、-1 | C、-2 | D、-4 |
化简（
+tanα）cosα等于（ ）
| 1 |
| tanα |
| A、tanα | ||
B、
| ||
| C、cosα | ||
D、
|