题目内容
14.化简多项式(2x+1)5-5(2x+1)4+10(2x+1)3-10(2x+1)2+5(2x+1)-1的结果是( )| A. | (2x+2)5 | B. | 2x5 | C. | (2x-1)5 | D. | 32x5 |
分析 利用二项式展开式的通项公式,以及二项式定理,求得结果.
解答 解:多项式(2x+1)5-5(2x+1)4+10(2x+1)3-10(2x+1)2+5(2x+1)-1
=[(2x+1)-1]5=32x5,
故选:D.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.将函数$y=3sin(2x+\frac{π}{6})$的图象上各点沿x轴向右平移$\frac{π}{6}$个单位长度,所得函数的解析式为( )
| A. | $y=3sin(2x-\frac{π}{6})$ | B. | y=3cos2x | C. | $y=3sin(2x+\frac{π}{3})$ | D. | y=3sin2x |
6.已知F1、F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,|PF1|=2|PF2|,则△F1PF2的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
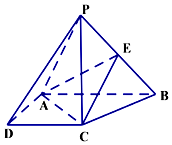 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.