题目内容
若log2x=a，则x= ．
考点：指数式与对数式的互化
专题：函数的性质及应用
分析：利用指数式与对数式的关系即可得出．
解答：
解：∵log2x=a，
∴x=2a．
故答案为：2a．
∴x=2a．
故答案为：2a．
点评：本题考查了指数式与对数式的关系，属于基础题．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
若
＜θ＜
，则下列不等式成立的是（ ）
| π |
| 4 |
| π |
| 3 |
| A、sinθ＞cosθ＞tanθ |
| B、cosθ＞tanθ＞sinθ |
| C、sinθ＞tanθ＞cosθ |
| D、tanθ＞sinθ＞cosθ |
已知点A（0，1），B（-2，3）C（-1，2），D（1，5），则向量
在
方向上的投影为（ ）
| AC |
| BD |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
设f（x）=x（x-1）（x-2）…（x-2015），则f′（2015）=（ ）
| A、-2013！ |
| B、-2015！ |
| C、2013！ |
| D、2015！ |
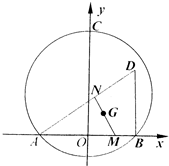在平面直角坐标系xOy中，已知点A（-1，0），B（1，0），C（0，a）（a∈R且a≠0），且动点D满足DA=