题目内容
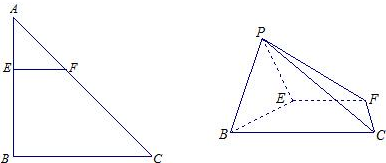
已知Rt△ABC中,∠B=90°,BA=BC=2,E,F分别是AB,AC的中点,把△AEF沿EF折起,使得点A至点P的位置,如图所示
(1)若PC=
,证明:PE⊥FC;
(2)若PB与平面BCFE所成角为30°,求平面PBE与平面PCF所成角的正切值.
(1)若PC=
| 6 |
(2)若PB与平面BCFE所成角为30°,求平面PBE与平面PCF所成角的正切值.

考点:二面角的平面角及求法,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(1)由已知得折起后EF⊥PE,EF⊥BE,从而BC⊥BE,BC⊥PB,进而得到BE⊥PE,由此能证明PE⊥FC.
(2)由已知得EF⊥平面PBE,从而平面PBE⊥平面BCFE,过P作PO⊥平面BCFE,交BE延长线于点O,以O为原点,OB为x轴,OP为z轴,建立空间直角坐标系,求出平面PCF的法向量和平面PBE的法向量,利用向量法能求出平面PBE与平面PCF所成角的正切值.
(2)由已知得EF⊥平面PBE,从而平面PBE⊥平面BCFE,过P作PO⊥平面BCFE,交BE延长线于点O,以O为原点,OB为x轴,OP为z轴,建立空间直角坐标系,求出平面PCF的法向量和平面PBE的法向量,利用向量法能求出平面PBE与平面PCF所成角的正切值.
解答:
(1)证明:∵Rt△ABC中,∠B=90°,BA=BC=2,
E,F分别是AB,AC的中点,
∴折起后EF⊥PE,EF⊥BE,
∵BC∥EF,∴BC⊥BE,BC⊥PB,
∵PC=
,∴PB=
=
,
∵BE=PE=1,∴BE2+PE2=PB2,∴BE⊥PE,
∴PE⊥平面BCFE,又FC?平面BCFE,
∴PE⊥FC.
(2)解:由(1)知EF⊥PE,EF⊥BE,又BE∩PE=E,
∴EF⊥平面PBE,又EF?平面BCFE,∴平面PBE⊥平面BCFE,
过P作PO⊥平面BCFE,交BE延长线于点O,
∵PB与平面BCFE所成角为30°,∴∠PBE=∠EPB=30°,
PB=
=
,
∴PO=
,BO=
,
以O为原点,OB为x轴,OP为z轴,建立空间直角坐标系,
P(0,0,
),C(
,2,0),F(
,1,0),
=(
,2,-
),
=(
,1,-
),
设平面PCF的法向量
=(x,y,z),
则
,取x=1,得
=(1,-1,-
),
又平面PBE的法向量
=(0,1,0),
设平面PBE与平面PCF所成角为θ,
cosθ=
=
=
,sinθ=
=
,
∴tanθ=
=
.
∴平面PBE与平面PCF所成角的正切值为
.

E,F分别是AB,AC的中点,
∴折起后EF⊥PE,EF⊥BE,
∵BC∥EF,∴BC⊥BE,BC⊥PB,
∵PC=
| 6 |
| 6-4 |
| 2 |
∵BE=PE=1,∴BE2+PE2=PB2,∴BE⊥PE,
∴PE⊥平面BCFE,又FC?平面BCFE,
∴PE⊥FC.
(2)解:由(1)知EF⊥PE,EF⊥BE,又BE∩PE=E,
∴EF⊥平面PBE,又EF?平面BCFE,∴平面PBE⊥平面BCFE,
过P作PO⊥平面BCFE,交BE延长线于点O,
∵PB与平面BCFE所成角为30°,∴∠PBE=∠EPB=30°,
PB=
| 1+1-2×1×1×cos120° |
| 3 |
∴PO=
| ||
| 2 |
| 3 |
| 2 |
以O为原点,OB为x轴,OP为z轴,建立空间直角坐标系,
P(0,0,
| ||
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| PC |
| 3 |
| 2 |
| ||
| 2 |
| PF |
| 1 |
| 2 |
| ||
| 2 |
设平面PCF的法向量
| n |
则
|
| n |
| ||
| 3 |
又平面PBE的法向量
| m |
设平面PBE与平面PCF所成角为θ,
cosθ=
|
| ||||
|
|
| 1 | ||
|
| 3 |
| 7 |
1-(
|
2
| ||
| 7 |
∴tanθ=
| sinθ |
| cosθ |
2
| ||
| 3 |
∴平面PBE与平面PCF所成角的正切值为
2
| ||
| 3 |
点评:本题主要考查直线与平面之间的平行、垂直等位置关系,空间向量、二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力.

练习册系列答案
相关题目
已知高为1的梯形ABCD内接于半径为1的圆O,若梯形的上底CD=1,则(
+
)•
=( )
| OA |
| OB |
| OC |
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
空间中有四点A,B,C,D,其中
=(2m,m,2),
=(m,m+1,-5),且
+
=(5,
,-3),则直线AB和CD( )
| AB |
| CD |
| AB |
| CD |
| 13 |
| 3 |
| A、平行 | B、异面 |
| C、必定相交 | D、必定垂直 |
若曲线y=x2+ax+b在点(1,1)处的切线为3x-y-2=0,则有( )
| A、a=-1,b=1 |
| B、a=-1,b=-1 |
| C、a=-2,b=1 |
| D、a=2,b=-1 |