题目内容
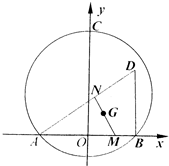 在平面直角坐标系xOy中,已知点A(-1,0),B(1,0),C(0,a)(a∈R且a≠0),且动点D满足DA=
在平面直角坐标系xOy中,已知点A(-1,0),B(1,0),C(0,a)(a∈R且a≠0),且动点D满足DA=| 3 |
(1)求过A,B,C三点的⊙Q的方程;
(2)当△DAB面积取到最大值
| 3 |
①若此时动点D又在⊙Q内(包含边界),求实数a的取值范围;
②设点G为△DAB的重心,过G作直线分别交边AB,AD于点M,N,求四边形MNDB的面积的最大值.
考点:圆的一般方程,平面向量的基本定理及其意义,平面向量数量积的运算
专题:平面向量及应用,直线与圆
分析:(1)设⊙Q方程为x2+y2+Dx+Ey+F=0,由题意,联立方程组
,解出即可得出.
(2)设D(x,y),由DA=
DB得,(x-2)2+y2=3,可得动点D的轨迹是以(2,0)为圆心,以
为半径的圆.可得△DAB中,底边AB上的高的最大值为
.
△DAB面积的最大值为
,此时D点坐标为(2,±
).
①由题意知,必有点(2,
)在⊙Q内(包含边界)或者点(2,-
)在⊙Q内(包含边界),代入⊙Q的方程得22+(
)2+
×
-1≤0或22+(-
)2+
(-
)-1≤0,解出即可得出a的取值范围.
②如图,设AM=pAB,AN=qAD,
=
=pq,点E为BD中点,G为△DAB重心,则AG=
AE.又
=
(
p+
q),则pq=
(p+q),由基本不等式得pq≥
,则S△AMN≥
S△ABD,从而有S四边形MNBD=S△ABD-S△AMN≤
S△ABD,即可得出.
|
(2)设D(x,y),由DA=
| 3 |
| 3 |
| 3 |
△DAB面积的最大值为
| 3 |
| 3 |
①由题意知,必有点(2,
| 3 |
| 3 |
| 3 |
| 1-a2 |
| a |
| 3 |
| 3 |
| 1-a2 |
| a |
| 3 |
②如图,设AM=pAB,AN=qAD,
| S△AMN |
| S△ABD |
| ||
|
| 2 |
| 3 |
| S△AMN |
| S△ABD |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| pq |
| 4 |
| 9 |
| 5 |
| 9 |
解答:
 解:(1)设⊙Q方程为x2+y2+Dx+Ey+F=0,
解:(1)设⊙Q方程为x2+y2+Dx+Ey+F=0,
由题意,联立方程组
,
解得D=0,E=
,F=-1.
∴⊙Q的方程为x2+y2+
y-1=0.
(2)设D(x,y),由题意得
=
,
化简得,(x-2)2+y2=3,
∵动点D的轨迹是以(2,0)为圆心,以
为半径的圆,
∴△DAB中,底边AB上的高的最大值为
.
∴△DAB面积的最大值为
,
此时D点坐标为(2,±
).
①由题意知,必有点(2,
)在⊙Q内(包含边界)或者点(2,-
)在⊙Q内(包含边界),
由(1)知⊙Q的方程为x2+y2+
y-1=0.
代入得22+(
)2+
×
-1≤0或22+(-
)2+
(-
)-1≤0,
化简得
≥0或
≤0,
解得a∈[
-2,0)∪[2+
,+∞);或a∈(-∞,-2-
]∪(0,2-
],
∴a∈(-∞,-2-
]∪(0,2-
]∪[
-2,0)∪[2+
,+∞).
②如图,设AM=pAB,AN=qAD,
=
=pq,
点E为BD中点,G为△DAB重心,则AG=
AE.
又
=
+
=
(
+
)=
(
p+
q),
则pq=
(p+q),由基本不等式得pq≥
,
解得pq≥
,当且仅当“p=q=
”时取“=”,
则S△AMN≥
S△ABD,从而有S四边形MNBD=S△ABD-S△AMN≤
S△ABD,
∵S△ABD的最大值为
,
综上可得有S四边形MNBD≤
S△ABD=
,即四边形MNBD的面积的最大值为
,
当且仅当MN∥BD时取“=”.
 解:(1)设⊙Q方程为x2+y2+Dx+Ey+F=0,
解:(1)设⊙Q方程为x2+y2+Dx+Ey+F=0,由题意,联立方程组
|
解得D=0,E=
| 1-a2 |
| a |
∴⊙Q的方程为x2+y2+
| 1-a2 |
| a |
(2)设D(x,y),由题意得
| (x+1)2+y2 |
| 3 |
| (x-1)2+y2 |
化简得,(x-2)2+y2=3,
∵动点D的轨迹是以(2,0)为圆心,以
| 3 |
∴△DAB中,底边AB上的高的最大值为
| 3 |
∴△DAB面积的最大值为
| 3 |
此时D点坐标为(2,±
| 3 |
①由题意知,必有点(2,
| 3 |
| 3 |
由(1)知⊙Q的方程为x2+y2+
| 1-a2 |
| a |
代入得22+(
| 3 |
| 1-a2 |
| a |
| 3 |
| 3 |
| 1-a2 |
| a |
| 3 |
化简得
a2-2
| ||
| a |
a2+2
| ||
| a |
解得a∈[
| 3 |
| 3 |
| 3 |
| 3 |
∴a∈(-∞,-2-
| 3 |
| 3 |
| 3 |
| 3 |
②如图,设AM=pAB,AN=qAD,
| S△AMN |
| S△ABD |
| ||
|
点E为BD中点,G为△DAB重心,则AG=
| 2 |
| 3 |
又
| S△AMN |
| S△ABD |
| S△AMG |
| S△ABD |
| S△ANG |
| S△ABD |
| 1 |
| 2 |
| S△AMG |
| S△ABE |
| S△ANG |
| S△ADE |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
则pq=
| 1 |
| 3 |
| 2 |
| 3 |
| pq |
解得pq≥
| 4 |
| 9 |
| 2 |
| 3 |
则S△AMN≥
| 4 |
| 9 |
| 5 |
| 9 |
∵S△ABD的最大值为
| 3 |
综上可得有S四边形MNBD≤
| 5 |
| 9 |
5
| ||
| 9 |
5
| ||
| 9 |
当且仅当MN∥BD时取“=”.
点评:本题考查了圆的标准方程、一元二次不等式的解法、三角形重心的性质、三角形的面积之比,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
抛物线x2=4y的准线l与y轴交于点P,若l绕点P以每秒
弧度的角速度按逆时针方向旋转t1秒后,恰好与抛物线第一次相交于一点,再旋转t2秒后,恰好与抛物线第二次相相交于一点,则t2的值为( )
| π |
| 12 |
| A、6 | B、4 | C、3 | D、2 |
复数z=
(i是虚数单位)的共轭复数为( )
| 5i |
| (2-i)(2+i) |
| A、i | ||
| B、-i | ||
C、
| ||
D、-
|
若曲线y=x2+ax+b在点(1,1)处的切线为3x-y-2=0,则有( )
| A、a=-1,b=1 |
| B、a=-1,b=-1 |
| C、a=-2,b=1 |
| D、a=2,b=-1 |
 如图,正方体ABCD-A1B1C1D1的棱长为1,E为棱DD1上的点,F为AB的中点,则三棱锥B1-BFE的体积为
如图,正方体ABCD-A1B1C1D1的棱长为1,E为棱DD1上的点,F为AB的中点,则三棱锥B1-BFE的体积为