题目内容
20.若函数f(x)=sin(x-θ)(θ>0)的图象关于直线x=$\frac{π}{6}$对称,则θ的最小值为$\frac{2π}{3}$.分析 令$\frac{π}{6}-θ$=$\frac{π}{2}+kπ$,解出θ,结合θ>0求出θ的最小值.
解答 解:∵f(x)的图象关于直线x=$\frac{π}{6}$对称,∴f($\frac{π}{6}$)=sin($\frac{π}{6}-θ$)=±1,
∴$\frac{π}{6}-θ$=$\frac{π}{2}+kπ$,∴θ=-$\frac{π}{3}$-kπ,k∈Z.∵θ>0,∴当k=-1时θ取得最小值$\frac{2π}{3}$.
故答案为$\frac{2π}{3}$.
点评 本题考查了正弦函数的对称轴,属于基础题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
10.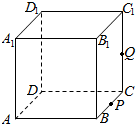 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的中点,则四面体A1PQD的正视图、侧视图和俯视图的面积之和为( )
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的中点,则四面体A1PQD的正视图、侧视图和俯视图的面积之和为( )
 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的中点,则四面体A1PQD的正视图、侧视图和俯视图的面积之和为( )
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的中点,则四面体A1PQD的正视图、侧视图和俯视图的面积之和为( )| A. | $\frac{5}{4}$ | B. | 2 | C. | $\frac{9}{4}$ | D. | $\frac{5}{2}$ |
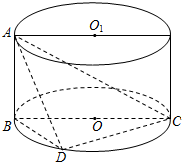 如图所示,圆柱O1O中,母线AB与底面垂直,BC是⊙O的直径,点D是⊙O的圆周上异于B,C的点.
如图所示,圆柱O1O中,母线AB与底面垂直,BC是⊙O的直径,点D是⊙O的圆周上异于B,C的点. 如图,在三棱柱ABC-A1B1C1中,AA1=A1C,D,E,F分别为AB,A1C1,AA1的中点,平面AA1C1C⊥平面ABC.G,H分别在AD,AC上,且AD=4AG,GH∥CD.求证:
如图,在三棱柱ABC-A1B1C1中,AA1=A1C,D,E,F分别为AB,A1C1,AA1的中点,平面AA1C1C⊥平面ABC.G,H分别在AD,AC上,且AD=4AG,GH∥CD.求证: