题目内容
18．已知sin（x+$\frac{π}{3}$）=$\frac{1}{3}$，则cosx+cos（$\frac{π}{3}$-x）的值为（ ）| A． | -$\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | -$\frac{1}{3}$ | D． | $\frac{1}{3}$ |
分析 根据两角和差的余弦公式和正弦公式计算即可．
解答 解：cosx+cos（$\frac{π}{3}$-x）=cosx+$\frac{1}{2}$cosx+$\frac{\sqrt{3}}{2}$sinx=$\frac{3}{2}$cosx+$\frac{\sqrt{3}}{2}$sinx=$\sqrt{3}$sin（x+$\frac{π}{3}$）=$\frac{\sqrt{3}}{3}$，
故选：B．
点评 本题考查了两角和差的余弦公式和正弦公式，属于基础题．
练习册系列答案
相关题目
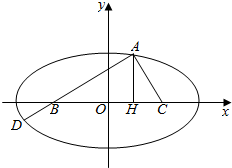如图，B（-c，0），C（c，0），AH⊥BC，垂足为H，且$\overrightarrow{BH}$=3$\overrightarrow{HC}$．又$\overrightarrow{AD}$=-4$\overrightarrow{DB}$，且A、D同在B、C为焦点的椭圆上，求椭圆的离心率．
13．已知函数f（x）满足f（2x）=x，则f（3）=（ ）
| A． | 0 | B． | 1 | C． | log23 | D． | 3 |