题目内容
已知函数f(x)=(
)x,等比数列{an}的前n项和为f(n)-c,数列{bn}{bn>0}的首项为c,且前n项和Sn满足Sn-Sn-1=
+
(n≥2).
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)若数列{
}前n项和为Tn,问使Tn>
的最小正整数n是多少?
| 1 |
| 3 |
| Sn |
| Sn-1 |
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)若数列{
| 1 |
| bnbn+1 |
| 1005 |
| 2014 |
考点:等差数列与等比数列的综合,数列的求和,数列递推式
专题:综合题,等差数列与等比数列
分析:(Ⅰ)利用n≥2时,an=[f(n)-c]-[f(n-1)-c],求数列{an}的通项公式;确定{
}是首项为1,公差为1的等差数列,可求{bn}的通项公式;
(Ⅱ)利用裂项法求数列的和,结合Tn>
,可求最小正整数n的值.
| Sn |
(Ⅱ)利用裂项法求数列的和,结合Tn>
| 1005 |
| 2014 |
解答:
解:(Ⅰ)∵函数f(x)=(
)x,等比数列{an}的前n项和为f(n)-c,
∴n≥2时,an=[f(n)-c]-[f(n-1)-c]=-
,
∴等比数列{an}的公比为q=
,
∴c=1,a1=-
,
∴an=-
;
∵数列{bn}{bn>0}的首项为c,且前n项和Sn满足Sn-Sn-1=
+
(n≥2).
∴b1=1,
-
=1,
∴{
}是首项为1,公差为1的等差数列,
∴
=n,
∴Sn=n2,
∴n≥2时,bn=Sn-Sn-1=2n-1,
∵b1=1,
∴bn=2n-1;
(Ⅱ)
=
(
-
),
∴Tn=
(1-
+
-
+…+
-
)=
(1-
)=
,
由Tn>
,得
>
,解得n>251.25
∴Tn>
的最小正整数n是252.
| 1 |
| 3 |
∴n≥2时,an=[f(n)-c]-[f(n-1)-c]=-
| 2 |
| 3n |
∴等比数列{an}的公比为q=
| 1 |
| 3 |
∴c=1,a1=-
| 2 |
| 3 |
∴an=-
| 2 |
| 3n |
∵数列{bn}{bn>0}的首项为c,且前n项和Sn满足Sn-Sn-1=
| Sn |
| Sn-1 |
∴b1=1,
| Sn |
| Sn-1 |
∴{
| Sn |
∴
| Sn |
∴Sn=n2,
∴n≥2时,bn=Sn-Sn-1=2n-1,
∵b1=1,
∴bn=2n-1;
(Ⅱ)
| 1 |
| bnbn+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
由Tn>
| 1005 |
| 2014 |
| n |
| 2n+1 |
| 1005 |
| 2014 |
∴Tn>
| 1005 |
| 2014 |
点评:本题考查数列的通项与求和,考查裂项法的运用,掌握数列通项的特点,选择正确的求和方法是关键.

练习册系列答案
相关题目
若角α的终边过点(-1,2),则cos2α的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知集合A={2a},B={a,b),若A∩B={
},则A∪B为( )
| 1 |
| 2 |
A、{
| ||
B、{-1,
| ||
C、{
| ||
D、{-1,
|
已知命题p:若非零实数a,b,则
<
;命题q:对任意实数x∈(0,+∞),log
(x+1)<0,则下列命题为真命题的是( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| A、p且q | B、p或¬q |
| C、¬p且q | D、p且¬q |
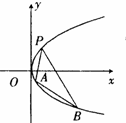 如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.
如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.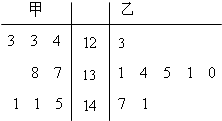 为了解某校高一学生的中考数学成绩,分别从甲乙两班随机各抽取8名学生的中考数学成绩,获得如图所示的茎叶图.
为了解某校高一学生的中考数学成绩,分别从甲乙两班随机各抽取8名学生的中考数学成绩,获得如图所示的茎叶图.