题目内容
已知函数f(x)=|x+1|-|x|+a.
(1)若a=0,求不等式f(x)≥0的解集;
(2)若不等式f(x)≤2恒成立,求实数a的取值范围.
(1)若a=0,求不等式f(x)≥0的解集;
(2)若不等式f(x)≤2恒成立,求实数a的取值范围.
考点:绝对值不等式的解法,函数恒成立问题
专题:不等式
分析:(1)将a=0代入函数的表达式|x+1|≥|x|,两边平方解出即可;(2)通过讨论x≤-1时,-1<x≤0时,x>0时的情况,从而求出a的范围.
解答:
解:(1)若a=0,则f(x)=|x+1|-|x|≥0,
∴|x+1|≥|x|,
∴(x+1)2≥x2,解得:x≥-
,
∴不等式f(x)≥0的解集是{x|x≥-
};
(2)x≤-1时,f(x)=a-1≤2,解得:a≤3①,
-1<x≤0时,f(x)=2x+1+a≤2,
∴a≤1-2x在(-1,0]恒成立,
而函数y=1-2x在(-1,0]的最小值是1,
∴a≤1②,
x>0时,f(x)=x+1-x+a≤2,解得:a≤1③,
综合①②③得:a≤1.
∴|x+1|≥|x|,
∴(x+1)2≥x2,解得:x≥-
| 1 |
| 2 |
∴不等式f(x)≥0的解集是{x|x≥-
| 1 |
| 2 |
(2)x≤-1时,f(x)=a-1≤2,解得:a≤3①,
-1<x≤0时,f(x)=2x+1+a≤2,
∴a≤1-2x在(-1,0]恒成立,
而函数y=1-2x在(-1,0]的最小值是1,
∴a≤1②,
x>0时,f(x)=x+1-x+a≤2,解得:a≤1③,
综合①②③得:a≤1.
点评:本题考查了绝对值不等式的解法,考查了函数恒成立问题,考查了分类讨论思想,是一道中档题.

练习册系列答案
相关题目
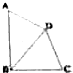 已知在四边形ABCD中,∠ABC=90°,BD平分∠ABC,∠ADC=135°,BC=8,AB=9,求CD的长.
已知在四边形ABCD中,∠ABC=90°,BD平分∠ABC,∠ADC=135°,BC=8,AB=9,求CD的长.