题目内容
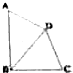已知在四边形ABCD中，∠ABC=90°，BD平分∠ABC，∠ADC=135°，BC=8，AB=9，求CD的长．考点：解三角形
专题：解三角形
分析：设∠BDC=θ，在△ABD与△BCD中，由正弦定理可得：
=
，
=
，可得sinθ=2cosθ，θ∈(0，
)．又sin2θ+cos2θ=1，解得sinθ=
．在△BCD中，由正弦定理可得
=
，即可得出．
| 9 |
| sin(135°-θ) |
| BD |
| sinθ |
| 8 |
| sinθ |
| BD |
| sin(135°-θ) |
| π |
| 2 |
2
| ||
| 5 |
| DC |
| sin45° |
| 8 |
| sinθ |
解答：
解：设∠BDC=θ，在△ABD与△BCD中，由正弦定理可得：
=
，
=
，
∴
=
，化为3sinθ=2
sin（135°-θ），
展开化为3sinθ=2
(
cosθ+
sinθ)，
∴sinθ=2cosθ，
可得θ∈(0，
)．
又sin2θ+cos2θ=1，
解得sinθ=
．
在△BCD中，由正弦定理可得
=
，
∴DC=
=
=2
．
| 9 |
| sin(135°-θ) |
| BD |
| sinθ |
| 8 |
| sinθ |
| BD |
| sin(135°-θ) |
∴
| 9sinθ |
| 8sin(135°-θ) |
| sin(135°-θ) |
| sinθ |
| 2 |
展开化为3sinθ=2
| 2 |
| ||
| 2 |
| ||
| 2 |
∴sinθ=2cosθ，
可得θ∈(0，
| π |
| 2 |
又sin2θ+cos2θ=1，
解得sinθ=
2
| ||
| 5 |
在△BCD中，由正弦定理可得
| DC |
| sin45° |
| 8 |
| sinθ |
∴DC=
| 8sin45° |
| sinθ |
8×
| ||||
|
| 10 |
点评：本题考查了正弦定理解三角形、同角三角函数基本关系式，考查了推理能力与计算能力，属于难题．
练习册系列答案
阅读快车系列答案
相关题目
若x、y满足不等式
，则（2x+y）2的最小值（ ）
|
| A、-4 | B、16 | C、4 | D、0 |
如图，延长△ABC的边BC到D，若tanB=| 5 |
| 8 |
| 1 |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
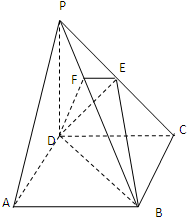如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F，求证：PF=若函数f（x）=
，则f（
）的值为（ ）
|
| 1 |
| 2 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|