题目内容
求证:
(1)2(1-sinα)(1+cosα)=(1-sinα+cosα)2
(2)sin2α+sin2β-sin2α•sin2β+cos2αcos2β=1.
(1)2(1-sinα)(1+cosα)=(1-sinα+cosα)2
(2)sin2α+sin2β-sin2α•sin2β+cos2αcos2β=1.
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:利用同角的三角函数的基本关系式从等式的一边入手证明得到另一边.
解答:
证明:(1)(1-sinα+cosα)2=1+sin2α+cos2α-2sinα+2cosα-2sinαcosα=2(1-sinα+cosα-sinαcosα)=2(1-sinα)(1+cosα)=右边;
(2)右边=sin2α+sin2β-sin2α•sin2β+cos2αcos2β
=(sin2α-sin2α•sin2β)+(sin2β+cos2αcos2β)
=sin2α(1-sin2β)+sin2β+cos2αcos2β
=sin2αcos2β+sin2β+cos2αcos2β
=sin2αcos2β+cos2αcos2β+sin2β
=cos2β+sin2β
=1=右边.
(2)右边=sin2α+sin2β-sin2α•sin2β+cos2αcos2β
=(sin2α-sin2α•sin2β)+(sin2β+cos2αcos2β)
=sin2α(1-sin2β)+sin2β+cos2αcos2β
=sin2αcos2β+sin2β+cos2αcos2β
=sin2αcos2β+cos2αcos2β+sin2β
=cos2β+sin2β
=1=右边.
点评:本题考查了同角三角函数的基本关系式的运用证明三角恒等式,属于基础题.

练习册系列答案
相关题目
若x、y满足不等式
,则(2x+y)2的最小值( )
|
| A、-4 | B、16 | C、4 | D、0 |
已知sinx+2cosx=-
,则tanx=( )
| 5 |
A、
| ||
| B、2 | ||
C、-
| ||
| D、-2 |
 如图,延长△ABC的边BC到D,若tanB=
如图,延长△ABC的边BC到D,若tanB=| 5 |
| 8 |
| 1 |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
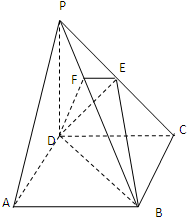 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F,求证:PF=
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F,求证:PF=