题目内容
若f(x)=
则方程f(x)=1的解的个数为: .
|
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:画出图象,求出当x<0时,f(x)=1,即x=-1,f(x)=1有1个解,当0≤x≤π时,f(x)=1,运用图象判断即可.
解答:
解:f(x)=

当x<0时,f(x)=1,即x=-1,1个解.
当0≤x≤π时,f(x)=1,x2=2sinx,1个解.

∴方程f(x)=1的所有解的个数2个
故答案为:2
|

当x<0时,f(x)=1,即x=-1,1个解.
当0≤x≤π时,f(x)=1,x2=2sinx,1个解.

∴方程f(x)=1的所有解的个数2个
故答案为:2
点评:本题考查了函数的性质,运用图象判断函数的单调性,结合图象判断交点个数,得出零点个数.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
下列函数在(0,+∞)上单调递增的是( )
| A、y=(x-1)2 | ||
| B、y=lg(x+3) | ||
| C、y=21-x | ||
D、y=
|
函数f(x)=2x-
-m的一个零点在区间(1,3)内,则实数m的取值范围是( )
| 3 |
| x |
| A、(-1,7) |
| B、(0,5) |
| C、(-7,1) |
| D、(1,5) |
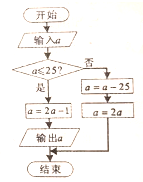 某班有49位同学玩“数字接龙”游戏,具体规则按如图所示的程序框图执行(其中a为座位号),并以输出的值作为下一个输入的值,若第一次 输入的值为8,则第三次输出的值为( )
某班有49位同学玩“数字接龙”游戏,具体规则按如图所示的程序框图执行(其中a为座位号),并以输出的值作为下一个输入的值,若第一次 输入的值为8,则第三次输出的值为( )