题目内容
已知tanα,tanβ是一元二次方程3x2+5x-2=0的两根,且α∈(0,
),β∈(
,π),
(1)求cos(α-β)的值;
(2)求α+β的值.
| π |
| 2 |
| π |
| 2 |
(1)求cos(α-β)的值;
(2)求α+β的值.
考点:两角和与差的正切函数,同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)通过方程的根,求出α、β的正切函数值,利用两角和的正切函数,求出正切函数值,通过角的范围,求cos(α-β)的值;
(2)利用(1)的结果求出α+β的正切函数值,通过角的范围求解角的大小即可.
(2)利用(1)的结果求出α+β的正切函数值,通过角的范围求解角的大小即可.
解答:
解:(1)一元二次方程3x2+5x-2=0的两根为-2和
,α∈(0,
),β∈(
,π),
∴tanβ=-2,tanα=
--(2分)
∴tan(α-β)=
=7,
α-β∈(-π,-
)
∴cos(α-β)=-
=-
=-
-------(6分)
(2)∵tanβ=-2,tanα=
,
∴tan(α+β)=
=-1,-----------------------(8分)
∵α∈(0,
),β∈(
,π),
∴α+β∈(
,
)------(10分),
∴α+β=
--------------(12分)
| 1 |
| 3 |
| π |
| 2 |
| π |
| 2 |
∴tanβ=-2,tanα=
| 1 |
| 3 |
∴tan(α-β)=
| tanα-tanβ |
| 1+tanαtanβ |
α-β∈(-π,-
| π |
| 2 |
∴cos(α-β)=-
|
|
| ||
| 10 |
(2)∵tanβ=-2,tanα=
| 1 |
| 3 |
∴tan(α+β)=
| tanα+tanβ |
| 1-tanαtanβ |
∵α∈(0,
| π |
| 2 |
| π |
| 2 |
∴α+β∈(
| π |
| 2 |
| 3π |
| 2 |
∴α+β=
| 3π |
| 4 |
点评:不考查两角和的正切函数的应用,三角函数的化简求值,注意角的范围的求法,考查分析问题解决问题的能力.

练习册系列答案
相关题目
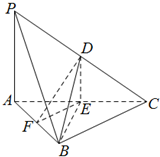 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5.
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5.