题目内容
已知点A(-
,0),B(
,0),且动点P满足|PA|-|PB|=2,则动点P的轨迹与直线y=k(x-2)有两个交点的充要条件为k∈ .
| 2 |
| 2 |
考点:双曲线的简单性质,必要条件、充分条件与充要条件的判断
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:运用双曲线的定义判断P的轨迹为A,B为焦点的双曲线的右支,求出方程,联立直线方程,消去y,得到二次方程,由条件可得该方程有两个正根,运用韦达定理和判别式,解不等式即可得到范围.
解答:
解:由点A(-
,0),B(
,0),则|AB|=2
,
动点P满足|PA|-|PB|=2<2
,
则由双曲线的定义,可得P的轨迹为A,B为焦点的双曲线的右支,
且有c=
,a=1,b=
=1,
方程为x2-y2=1(x>0),
联立直线y=k(x-2),得到(1-k2)x2+4k2x-4k2-1=0,
由于动点P的轨迹与直线y=k(x-2)有两个交点,
则该方程有两个正根.
设交点为(x1,y1),(x2,y2),则
判别式16k4+4(1-k2)(1+4k2)>0,即为1+3k2>0成立,
x1+x2=
>0,x1x2=
>0,
则由1-k2<0,解得,k>1或k<-1.
故答案为:(-∞,-1)∪(1,+∞).
| 2 |
| 2 |
| 2 |
动点P满足|PA|-|PB|=2<2
| 2 |
则由双曲线的定义,可得P的轨迹为A,B为焦点的双曲线的右支,
且有c=
| 2 |
| c2-a2 |
方程为x2-y2=1(x>0),
联立直线y=k(x-2),得到(1-k2)x2+4k2x-4k2-1=0,
由于动点P的轨迹与直线y=k(x-2)有两个交点,
则该方程有两个正根.
设交点为(x1,y1),(x2,y2),则
判别式16k4+4(1-k2)(1+4k2)>0,即为1+3k2>0成立,
x1+x2=
| -4k2 |
| 1-k2 |
| -4k2-1 |
| 1-k2 |
则由1-k2<0,解得,k>1或k<-1.
故答案为:(-∞,-1)∪(1,+∞).
点评:本题考查双曲线的定义和方程,考查直线和双曲线方程联立,消去未知数,运用韦达定理,考查运算能力,属于中档题和易错题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
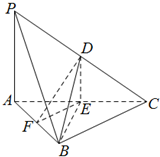 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5.
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5.