题目内容
函数f(x)=2x-
-m的一个零点在区间(1,3)内,则实数m的取值范围是( )
| 3 |
| x |
| A、(-1,7) |
| B、(0,5) |
| C、(-7,1) |
| D、(1,5) |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:根据函数解析式判断可判断(0,+∞)单调递增函数,零利用点的存在性定理,得出f(1)<0,f(3)>0,即可.
解答:
解:∵f(x)=2x-
-m,
∴可判断(0,+∞)单调递增函数,
∵f(x)=2x-
-m的一个零点在区间(1,3)内,
∴f(1)<0,f(3)>0,
即:m>-1且m<7,
-1<m<7
故选:A
| 3 |
| x |
∴可判断(0,+∞)单调递增函数,
∵f(x)=2x-
| 3 |
| x |
∴f(1)<0,f(3)>0,
即:m>-1且m<7,
-1<m<7
故选:A
点评:本题考查了函数的单调性,零点的存在性定理,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
“关于x的方程x4+ax2+b=0有解”是“关于x的方程x2+ax+b=0”的( )
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
先后抛掷两颗骰子,则所得点数之和为7的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设实数x、y,满足约束条件
,则z=2x+3y+1的最小值为( )
|
| A、27 | B、25 | C、17 | D、15 |
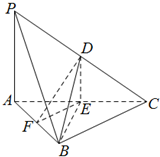 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5.
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5.