题目内容
下列函数在(0,+∞)上单调递增的是( )
| A、y=(x-1)2 | ||
| B、y=lg(x+3) | ||
| C、y=21-x | ||
D、y=
|
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:结合选项中所涉及到的函数,从函数的定义域和其图象上进行逐个排除即可得到答案.
解答:
解:对于选项A:y=(x-1)2
该函数在(-∞,1]上单调递减,在区间(1,+∞)上单调递增不合题意,
对于选项B:y=lg(x+3),
该函数在区间(0,+∞)上单调递增合题意,
对于选项C:y=21-x,
该函数在(-∞,+∞)上单调递减,不合题意,
对于选项D:y=(x-1)2
该函数在(-∞,-1)上单调递减,在区间(-1,+∞)上单调递减,不合题意,
故选:B.
该函数在(-∞,1]上单调递减,在区间(1,+∞)上单调递增不合题意,
对于选项B:y=lg(x+3),
该函数在区间(0,+∞)上单调递增合题意,
对于选项C:y=21-x,
该函数在(-∞,+∞)上单调递减,不合题意,
对于选项D:y=(x-1)2
该函数在(-∞,-1)上单调递减,在区间(-1,+∞)上单调递减,不合题意,
故选:B.
点评:本题重点考查了函数的单调性、及其判断,函数的图象等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知双曲线x2-
=1的两个焦点分别为F1、F2,点P为双曲线上一点,且∠F1PF2=90°,则△F1PF2的周长等于( )
| y2 |
| 3 |
| A、6 | ||
| B、8 | ||
C、4+2
| ||
D、2+2
|
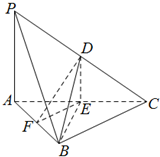 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5.
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5.