题目内容
 已知函数f(x)=sin(ωx-
已知函数f(x)=sin(ωx-| π |
| 4 |
(1)求f(
| π |
| 6 |
(2)在图3给定的平面直角坐标系中,画出函数y=f(x)在区间[-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
考点:五点法作函数y=Asin(ωx+φ)的图象,正弦函数的图象
专题:作图题,三角函数的图像与性质
分析:(1)依题意先解得ω=2,可得解析式f(x)=sin(2x-
),从而可求f(
)的值.
(2)先求范围2x-
∈[-
,
],列表,描点,连线即可五点法作图象,并根据图象写出其在(-
,
)上的单调递减区间.
| π |
| 4 |
| π |
| 6 |
(2)先求范围2x-
| π |
| 4 |
| 5π |
| 4 |
| 3π |
| 4 |
| π |
| 2 |
| π |
| 2 |
解答:
解:(1)依题意得
=π,解得ω=2,
∴f(x)=sin(2x-
),
∴f(
)=sin(
-
)=sin
cos
-cos
sin
=
×
-
×
=
(2)∵x∈[-
,
]
∴2x-
∈[-
,
],
列表如下:
画出函数y=f(x)在区间[-
,
]上的图象如下:
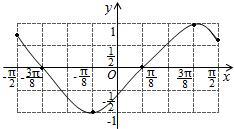
由图象可知函数y=f(x)在(-
,
)上的单调递减区间为(-
,-
),(
,
)
| 2π |
| ω |
∴f(x)=sin(2x-
| π |
| 4 |
∴f(
| π |
| 6 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||||
| 4 |
(2)∵x∈[-
| π |
| 2 |
| π |
| 2 |
∴2x-
| π |
| 4 |
| 5π |
| 4 |
| 3π |
| 4 |
列表如下:
2x-
| -
| -π | -
| 0 |
|
| ||||||||||||
| x | -
| -
| -
|
|
|
| ||||||||||||
| f(x) |
| 0 | -1 | 0 | 1 |
|
| π |
| 2 |
| π |
| 2 |

由图象可知函数y=f(x)在(-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 8 |
| 3π |
| 8 |
| π |
| 2 |
点评:本题主要考察了五点法作函数y=Asin(ωx+φ)的图象,三角函数的图象与性质,属于基础题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知复数z满足z(1+i)=1(其中i为虚数单位),则z=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知两条直线l1:y=m和l2:y=
(m>0),l1与函数y=|log2x|的图象从左至右相交于点A、B,l2与函数y=|log2x|的图象从左至右相交于C、D,记线段AC和BD在x轴上的投影长度分别为a、b,当m变化时,
的最小值为( )
| 4 |
| m+1 |
| b |
| a |
| A、16 | ||
| B、8 | ||
C、8
| ||
D、4
|
若函数y=f(x)是函数y=ax(a>0,且a≠1)的反函数,且f(3)=1,则f(x)=( )
| A、log3x | ||
B、
| ||
C、log
| ||
| D、3x-2 |
已知集合M={x∈R|0<x<2},N={x∈R|x>1},则M∩(∁RN)=( )
| A、[1,2) |
| B、(1,2) |
| C、[0,1) |
| D、(0,1] |