题目内容
6.已知矩阵A=$[\begin{array}{l}{1}&{0}\\{0}&{\sqrt{2}}\end{array}]$所对应的变换T把曲线C变成曲线C1:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1,求曲线C的方程.分析 根据矩阵变换得出变换前后坐标的变化规律,把变换后的坐标代入C1即可得出曲线C的方程.
解答 解:设曲线C上任一点为(x,y),经过变换T变成(x0,y0),
则$(\begin{array}{l}{1}&{0}\\{0}&{\sqrt{2}}\end{array})$$(\begin{array}{l}{x}\\{y}\end{array})$=$(\begin{array}{l}{{x}_{0}}\\{{y}_{0}}\end{array})$,∴$\left\{\begin{array}{l}{{x}_{0}=x}\\{{y}_{0}=\sqrt{2}y}\end{array}\right.$.
∵(x0,y0)在曲线C1:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1上,
∴$\frac{{{x}_{0}}^{2}}{4}+\frac{{{y}_{0}}^{2}}{2}$=1,即$\frac{{x}^{2}}{4}$+y2=1.
∴曲线C的方程是$\frac{{x}^{2}}{4}$+y2=1.
点评 本题考查了矩阵变换,属于基础题.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
1.已知i是虚数单位,复数z满足z=i(i-1),则z的虚部是( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
18.在△ABC中,a,b,c分别为三个内角A、B、C所对的,若$cosB=\frac{1}{4},b=2,sinC=2sinA$,则△ABC的面积为( )
| A. | $\frac{{\sqrt{15}}}{6}$ | B. | $\frac{{\sqrt{15}}}{4}$ | C. | $\frac{{\sqrt{15}}}{2}$ | D. | $\sqrt{15}$ |
15.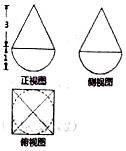 一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
 一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )| A. | $4+\frac{2π}{3}$ | B. | $4+\frac{{\sqrt{2}π}}{6}$ | C. | $2+\frac{2π}{3}$ | D. | $2+\frac{{\sqrt{2}π}}{6}$ |
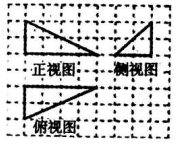 如图,网格纸上的小正方形边长为1,粗线画出的是某几何体的三视图,则该几何体外接球的体积为$8\sqrt{6}π$.
如图,网格纸上的小正方形边长为1,粗线画出的是某几何体的三视图,则该几何体外接球的体积为$8\sqrt{6}π$.