Question

15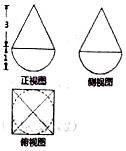．一个由半球和四棱锥组成的几何体，其三视图如图所示，则该几何体的体积为（　　）

• A． $4+\frac{2π}{3}$
• B． $4+\frac{{\sqrt{2}π}}{6}$
• C． $2+\frac{2π}{3}$
• D． $2+\frac{{\sqrt{2}π}}{6}$

Answer 1

分析 根据三视图求出半球的半径和四棱锥的底面边长和高，代入几何体的体积公式即可．

解答 解：由三视图可知半球的半径为1，四棱锥的底面为边长为2的正方形，棱锥的高为3，
∴几何体的体积V=$\frac{1}{2}×\frac{4}{3}π×{1}^{3}$+$\frac{1}{3}×{2}^{2}×3$=4+$\frac{2π}{3}$．
故选：A．

点评 本题考查了空间几何体的结构特征和三视图，几何体的体积计算，属于中档题．