题目内容
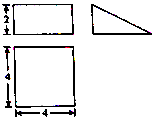
16.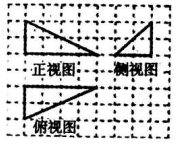 如图,网格纸上的小正方形边长为1,粗线画出的是某几何体的三视图,则该几何体外接球的体积为$8\sqrt{6}π$.
如图,网格纸上的小正方形边长为1,粗线画出的是某几何体的三视图,则该几何体外接球的体积为$8\sqrt{6}π$.
分析 作出几何体的直观图,建立坐标系,利用距离公式列方程求出外接球的球心坐标,从而得出外接球的半径,代入体积公式计算得出答案.
解答 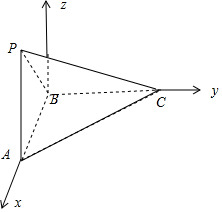 解:几何体为三棱锥,直观图如图所示:
解:几何体为三棱锥,直观图如图所示:
其中PA⊥底面ABC,AB⊥BC,BC=4,AB=PA=2,
以B为原点建立如图所示的空间坐标系B-xyz,
则A=(2,0,0),B(0,0,0),C(0,4,0),P(2,0,2),
设棱锥的外接球球心为M(x,y,z),则MA=MB=MC=MP,
即(x-2)2+y2+z2=x2+y2+z2=x2+(y-4)2+z2=(x-2)2+y2+(z-2)2,
∴x=1,y=2,z=1,
∴外接球半径R=|MB|=$\sqrt{{x}^{2}+{y}^{2}+{z}^{2}}$=$\sqrt{6}$.
∴外接球的体积V=$\frac{4}{3}π{R}^{3}$=8$\sqrt{6}$π.
故答案为:8$\sqrt{6}$π.
点评 本题考查了棱锥的三视图,棱锥与外接球的位置关系,体积公式,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
7.某几何体的三视图如图所示,则该几何体的体积为( )
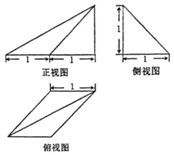

| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
4.已知某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | $\frac{27}{2}$ | B. | 27 | C. | $27\sqrt{2}$ | D. | $27\sqrt{3}$ |
11.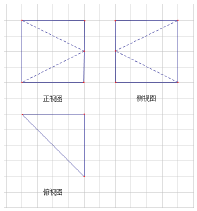 图中,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,且该几何体的顶点都在同一球面上,则该几何体的外接球的表面积为( )
图中,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,且该几何体的顶点都在同一球面上,则该几何体的外接球的表面积为( )
 图中,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,且该几何体的顶点都在同一球面上,则该几何体的外接球的表面积为( )
图中,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,且该几何体的顶点都在同一球面上,则该几何体的外接球的表面积为( )| A. | 32π | B. | 48π | C. | 50π | D. | 64π |
1.某三棱柱的三视图如图所示,该三棱柱的外接球的表面积为( )

| A. | 32+8$\sqrt{5}$ | B. | 36π | C. | 18π | D. | $\frac{40\sqrt{10}}{3}$π |