题目内容
17.把地球看作是半径为R的球,A点位于北纬30°,东经20°,B点位于北纬30°,东经80°,求A、B两点间的球面距离R•arccos$\frac{5}{8}$(结果用反三角表示)分析 设北纬30°纬线圈所在圆的圆心为O1,半径为r,则r=$\frac{\sqrt{3}}{2}$R,且△AO1B为等边三角形,即AB=$\frac{\sqrt{3}}{2}$R;△AOB中,由余弦定理求得∠AOB的值,利用弧长共公式求得A、B两点间的球面距离.
解答 解:设北纬30°纬线圈所在圆的圆心为O1,半径为r,则r=R•cos30°=$\frac{\sqrt{3}}{2}$R,
根据A点位于北纬30°,东经20°,B点位于北纬30°,东经80°,可得∠AO1B=60°,
∴△AO1B为等边三角形,即AB=r=$\frac{\sqrt{3}}{2}$R.
△AOB中,由余弦定理可得AB2=$\frac{3}{4}$R2=R2+R2-2R2•cos∠AOB,求得cos∠AOB=$\frac{5}{8}$,
∴∠AOB=arccos$\frac{5}{8}$,∴A、B两点间的球面距离 $\widehat{AB}$=R•∠AOB=R•arccos$\frac{5}{8}$,
故答案为:R•arccos$\frac{5}{8}$.
点评 本题主要考查球面距离的求法,利用余弦定理解三角形,反三角函数、弧长公式的应用,属于中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
7.某几何体的三视图如图所示,则该几何体的体积为( )
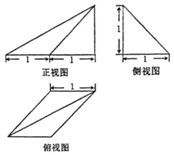

| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
9.已知等比数列{an}满足a1a2=1,a5a6=4,则a3a4=( )
| A. | 2 | B. | ±2 | C. | $\sqrt{2}$ | D. | $±\sqrt{2}$ |