题目内容
8.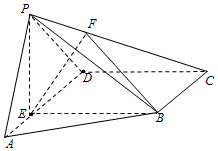 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.(Ⅰ)求证:PA∥平面BEF;
(Ⅱ)求三棱锥P-ABF与三棱锥F-EBC的体积之比.
分析 (Ⅰ)连接AC交BE于点M,连接FM.由AD∥BC,BC=ED,得BCDE为平行四边形,得EM∥CD,再由平行线截线段成比例可得FM∥AP.进一步由线面平行的判定得PA∥平面BEF;
(Ⅱ)利用等积法把三棱锥P-ABF与三棱锥F-EBC的体积之比转化为三棱锥A-PBF与三棱锥E-FBC的体积之比,进一步转化为线段PF与FC的长度比得答案.
解答 (Ⅰ)证明:连接AC交BE于点M,连接FM.
由AD∥BC,BC=ED,得BCDE为平行四边形,则EM∥CD,
∴$\frac{AM}{MC}=\frac{AE}{ED}=\frac{1}{2}=\frac{PF}{FC}$.
∴FM∥AP.
∵FM?平面BEF,PA?平面BEF,
∴PA∥平面BEF;
(Ⅱ)$\frac{{V}_{P-ABF}}{{V}_{F-EBC}}=\frac{{V}_{A-PBF}}{{V}_{E-BCF}}=\frac{{S}_{△PBF}}{{S}_{△FBC}}=\frac{PF}{FC}=\frac{1}{2}$.
点评 本题考查线面平行的判定,考查了利用等积法求多面体的体积,体现了数学转化思想方法,是中档题.

练习册系列答案
相关题目
19.设M=2a2-4a,N=a2-2a-3,则有( )
| A. | M<N | B. | M≤N | C. | M>N | D. | M≥N |
3.某公司今年一月份推出新产品A,其成本价为492元/件,经试销调查,销售量与销售价的关系如下表:
由此可知,销售量y(件)与销售价x(元/件)可近似看作一次函数y=kx+b的关系(通常取表中相距较远的两组数据所得一次函数较为精确).
(1)写出以x为自变量的函数y的解析式及定义域;
(2)试问:销售价定为多少时,一月份销售利润最大?并求最大销售利润和此时的销售量.
| 销售价(x/元件) | 650 | 662 | 720 | 800 |
| 销售量(y件) | 350 | 333 | 281 | 200 |
(1)写出以x为自变量的函数y的解析式及定义域;
(2)试问:销售价定为多少时,一月份销售利润最大?并求最大销售利润和此时的销售量.
18.原命题为“若a>b,则ac2>bc2”关于其逆命题,否命题,逆否命题 真假性的判断依次如下,正确的是( )
| A. | 真,真,真 | B. | 真,真,假 | C. | 假,假,真 | D. | 假,假,假 |
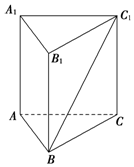 如图所示,在正三棱柱ABC-A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为30°,求该三棱柱的体积.
如图所示,在正三棱柱ABC-A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为30°,求该三棱柱的体积.