题目内容
13.正方体ABCD-A1B1C1D1中,E,F分别是AD,DD1的中点,AB=4,则过B,E,F的平面截该正方体所得的截面周长为( )| A. | 6$\sqrt{2}$+4$\sqrt{5}$ | B. | 6$\sqrt{2}$+2$\sqrt{5}$ | C. | 3$\sqrt{2}$+4$\sqrt{5}$ | D. | 3$\sqrt{2}$+2$\sqrt{5}$ |
分析 推导出EF∥平面BCC1,过EF且过B的平面与面BCC1的交线l平行于EF,l即为BC1.由此能求出过点B,E,F的平面截该正方体所得的截面周长.
解答 解:∵正方体ABCD-A1B1C1D1中,E、F分别是棱AD、DD1的中点,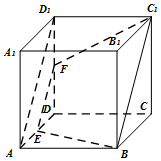
∴EF∥AD1∥BC1,
∵EF?平面BCC1,BC1?平面BCC1,
∴EF∥平面BCC1,
由线面平行性质定理,过EF且过B的平面与面BCC1的交线l平行于EF,l即为BC1.
由正方体的边长为4,可得截面是以BE=C1F=2$\sqrt{5}$为腰,EF=2$\sqrt{2}$为上底,BC1=2EF=4$\sqrt{2}$ 为下底的等腰梯形,故周长为6$\sqrt{2}$+4$\sqrt{5}$,
故选A.
点评 本题考查截面周长的求法,是中档题,解题时要认真审题,注意空间思维能力的培养,确定截面形状是关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
4.已知集合A={3,a2},B={2,1-a,b},且A∩B={1},则A∪B=( )
| A. | {0,1,3} | B. | {1,2,3} | C. | {1,2,4} | D. | {0,1,2,3} |
8.复数z=1-2i,$\overline{z}$是z的共轭复数,则复平面内复数z•$\overline{z}$-i对应的点所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.已知集合A={x|x2<4},B={x∈Z|-3≤x<1},则A∩B=( )
| A. | {-2,-1,0} | B. | (-1,0) | C. | {-1,0} | D. | (-3,-2) |
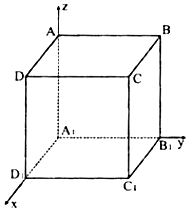 如图建立空间直角坐标系,已知正方体的棱长为2.
如图建立空间直角坐标系,已知正方体的棱长为2.