题目内容
2．已知函数$f（x）={log_2}\frac{{2（{1+x}）}}{x-1}$，若f（a）=2，则f（-a）=0．分析 由题意，f（a）+f（-a）=$lo{g}_{2}[\frac{2（1+a）}{a-1}•\frac{2（1-a）}{-a-1}]$=2，即可得出结论．
解答 解：由题意，f（a）+f（-a）=$lo{g}_{2}[\frac{2（1+a）}{a-1}•\frac{2（1-a）}{-a-1}]$=2，
∵f（a）=2，∴f（-a）=0，
故答案为0．
点评 本题考查函数的性质，考查对数的运算性质，比较基础．
练习册系列答案
相关题目
13．正方体ABCD-A1B1C1D1中，E，F分别是AD，DD1的中点，AB=4，则过B，E，F的平面截该正方体所得的截面周长为（ ）
| A． | 6$\sqrt{2}$+4$\sqrt{5}$ | B． | 6$\sqrt{2}$+2$\sqrt{5}$ | C． | 3$\sqrt{2}$+4$\sqrt{5}$ | D． | 3$\sqrt{2}$+2$\sqrt{5}$ |
7．已知$f（x）=sin（2017x+\frac{π}{6}）+cos（2017x-\frac{π}{3}）$的最大值为A，若存在实数x1，x2使得对任意实数x总有f（x1）≤f（x）≤f（x2）成立，则A|x1-x2|的最小值为（ ）
| A． | $\frac{π}{2017}$ | B． | $\frac{2π}{2017}$ | C． | $\frac{4π}{2017}$ | D． | $\frac{π}{4034}$ |
14．已知函数f（x）=x3-2x，则f（3）=（ ）
| A． | 1 | B． | 19 | C． | 21 | D． | 35 |
11．
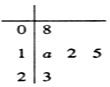如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图，若该运动员在这5场比赛中的得分的中位数为12，则该运动员这5场比赛得分的平均数不可能为（ ）
如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图，若该运动员在这5场比赛中的得分的中位数为12，则该运动员这5场比赛得分的平均数不可能为（ ）| A． | $\frac{68}{5}$ | B． | $\frac{69}{5}$ | C． | 14 | D． | $\frac{71}{5}$ |