题目内容
设a1,a2,…,an为正整数,其中至少有五个不同值,若对任意的i,j(1≤i<j≤n),存在k,l(k≠l,且异于i与j)使得ai+aj=ak+al,则n的最小值为 .
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:根据题意,设a1,a2,an为正整数,其中至少有五个不同值.若对于任意的i,j(1≤i<j≤n),存在k,l(k≠l,且异于i与j)使得ai+aj=ak+al,那么对于n至少大于等于5,那么对于n从6开始,逐一的验证可知,那么最小的n为13.
解答:
解:首先将这n个数从小到大排序,仍记为a1,a2,…an且a1≤a2≤…≤a1.
考虑n的最小值.首先这个数列的最大最小值数的个数必不少于4.
比如取i=n-1,j=n,要存在k,l使得ai+aj=ak+al,
由于其他数都小于等于ai,且ai≤aj,
必有ai=aj=ak=al,即至少有4个最大值,
同理必有4个最小值,再考虑中间的数.第二小的数至少有两个,
比如取最小的数和第二小的数,一定要存在k,l使得他们俩的和要等于第一小和第二小的数之和,
那么这两个数必也为最小的和第二小的数.
这样必有两个第二小的数,
同理第二大的数也至少有两个,由于至少有5个不同的值,
那么这样n的最小值即为4+2+1+2+4=13.
故答案为:13
考虑n的最小值.首先这个数列的最大最小值数的个数必不少于4.
比如取i=n-1,j=n,要存在k,l使得ai+aj=ak+al,
由于其他数都小于等于ai,且ai≤aj,
必有ai=aj=ak=al,即至少有4个最大值,
同理必有4个最小值,再考虑中间的数.第二小的数至少有两个,
比如取最小的数和第二小的数,一定要存在k,l使得他们俩的和要等于第一小和第二小的数之和,
那么这两个数必也为最小的和第二小的数.
这样必有两个第二小的数,
同理第二大的数也至少有两个,由于至少有5个不同的值,
那么这样n的最小值即为4+2+1+2+4=13.
故答案为:13
点评:本题主要考查数列的应用,解决的关键是理解任意和存在的含义,并能对于n令值来分析推导得到结论,难度较大.

练习册系列答案
相关题目
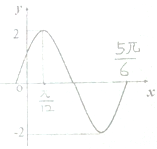 函数f(x)=Asin(ωx+φ)(ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(ω>0,|φ|<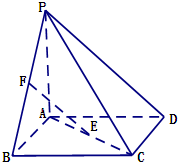 如图,四棱P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,E、F分别是AC、PB的中点.
如图,四棱P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,E、F分别是AC、PB的中点.