题目内容
某大学有本科生8000人，其中一、二、三、四年级的学生比为5：4：3：1，要用分层抽样的方法从所有本科生中抽取一个容量为260的样本，则应抽二年级的学生（ ）
| A、100人 | B、60人 |
| C、80人 | D、20人 |
考点：分层抽样方法
专题：概率与统计
分析：由一、二、三、四年级的学生比为5：4：3：1，要用分层抽样的方法从所有本科生中抽取一个容量为260的样本，能求出应抽二年级的学生人数．
解答：
解：∵大学有本科生8000人，其中一、二、三、四年级的学生比为5：4：3：1，
要用分层抽样的方法从所有本科生中抽取一个容量为260的样本，
∴应抽二年级的学生人数为：
260×
=80（人）．
故选：C．
要用分层抽样的方法从所有本科生中抽取一个容量为260的样本，
∴应抽二年级的学生人数为：
260×
| 4 |
| 5+4+3+1 |
故选：C．
点评：本题考查分层抽样的应用，解题时要认真审题，是基础题．
练习册系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
设火箭发射成功的概率为0.99，若发射10次，其中失败的次数为X，则E（X）等于（ ）
| A、0.01 | ||
| B、9.9 | ||
| C、0.1 | ||
D、C
|
有一段演绎推理是这样的：“若直线平行于平面，则该直线平行于平面内所有直线：已知直线b∥平面α，直线a?平面α，则直线b∥直线a”，结论显然是错误的，这是因为（ ）
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、非以上错误 |
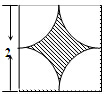如图所示，墙上挂有边长为2的正方形木板，它的四个角的空白部分都是以正方形的顶点为圆心，半径为1的圆孤，某人向此板投镖，假设每次都能击中木板，且击中木板上每个点的可能性都一样，则它击中阴影部分的概率是（ ）A、
| ||
B、
| ||
C、1-
| ||
D、1-
|
已知三棱锥的三视图如图所示，其中侧视图为直角三角形，俯视图为等腰直角三角形，则此三棱锥的体积等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（
-
）n的展开式中只有第5项的二项式系数最大，则展开式中的常数项是（ ）
| 3 | x |
| 1 |
| x |
| A、28 | B、-28 |
| C、70 | D、-70 |
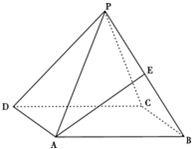正四棱锥P-ABCD中，侧面与底面ABCD所成的角为60°，E是PB的中点，求异面直线PD与AE所成角的大小．
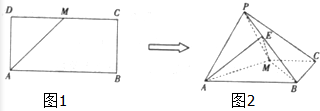如图，已知长方形ABCD中，AB=2，AD=1，M为DC的中点．将△ADM沿AM折起到△APM，使得平面APM⊥平面ABCM，点E在线段PB上，且PE=