题目内容
若f(x)=x(|x|-2)在区间[-2,m]上的最大值为1,则实数m的取值范围是 .
考点:函数的最值及其几何意义
专题:计算题,作图题,函数的性质及应用
分析:作函数f(x)=x(|x|-2)的图象,由图象知当f(x)=1时,x=-1或x=
+1;从而由图象求解.
| 2 |
解答:
解:作函数f(x)=x(|x|-2)的图象如下,

当f(x)=1时,x=-1或x=
+1;
故由图象可知,
实数m的取值范围是[-1,
+1].
故答案为:[-1,
+1].

当f(x)=1时,x=-1或x=
| 2 |
故由图象可知,
实数m的取值范围是[-1,
| 2 |
故答案为:[-1,
| 2 |
点评:本题考查了函数的图象的应用及最值的求法,属于基础题.

练习册系列答案
相关题目
曲线y=e
x在点(4,e2)处的切线与坐标轴所围三角形的面积为( )
| 1 |
| 2 |
| A、e2 | ||
| B、2e2 | ||
| C、4e2 | ||
D、
|
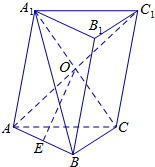 如图,斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是AB的中点.求证:
如图,斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是AB的中点.求证: