题目内容
表面积为4的正四棱锥的俯视图是边长为1的正方形,则其正视图面积最小值为 .
考点:简单空间图形的三视图
专题:空间位置关系与距离
分析:设侧面的斜高为x,根据表面积为4的正四棱锥的俯视图是边长为1的正方形,可得12+4×
×1×x=4,解得x.可得正四棱锥的高h=
.即可得出.
| 1 |
| 2 |
x2-(
|
解答:
解:设侧面的斜高为x,
∵表面积为4的正四棱锥的俯视图是边长为1的正方形,
∴12+4×
×1×x=4,解得x=
.
∴正四棱锥的高h=
=
.
∴其正视图面积最小值S=
×1×
=
.
故答案为:
.
∵表面积为4的正四棱锥的俯视图是边长为1的正方形,
∴12+4×
| 1 |
| 2 |
| 3 |
| 2 |
∴正四棱锥的高h=
x2-(
|
| 2 |
∴其正视图面积最小值S=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了轴四棱锥的三视图及其有关计算,属于基础题.

练习册系列答案
相关题目
已知全集U=R,集合M={x|-2≤x-1≤2},N={x|x=2k-1,k=1,2,…},则M∩N等于( )
| A、{1} |
| B、{1,3} |
| C、{-1,1,3} |
| D、{-1,0,1,3} |
在空间直角坐标系O-xyz中,在坐标平面xOy上到点A(3,2,50),B(3,5,1)距离相等的点有( )
| A、1个 | B、2个 |
| C、不存在 | D、无数个 |
曲线y=e
x在点(4,e2)处的切线与坐标轴所围三角形的面积为( )
| 1 |
| 2 |
| A、e2 | ||
| B、2e2 | ||
| C、4e2 | ||
D、
|
执行如图程序框图.若输入n=20,则输出的S值是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
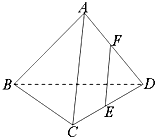 已知在空间四边形ABCD中,AC=AD,BC=BD,且E,F分别是CD,AD的中点.
已知在空间四边形ABCD中,AC=AD,BC=BD,且E,F分别是CD,AD的中点.