题目内容
已知x轴上有一列点P1,P2,P3,…,Pn,…,当n≥2时,点Pn是把线段Pn-1Pn+1作n等分的分点中最靠近Pn-1的点,设线段P1P2,P2P3,…,PnPn+1…的长度分别为a1,a2,a3,…,an…,其中a1=1.
(Ⅰ)写出a2,a3,a4;
(Ⅱ)证明:
+
+…+
<3 (n∈N*);
(Ⅲ)设点Mn(n,
)(n>2,n∈N*),在这些点中是否存在两个点同时在函数y=
(k>0)的图象上,如果存在,求出点的坐标;如果不存在,请说明理由.
(Ⅰ)写出a2,a3,a4;
(Ⅱ)证明:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
(Ⅲ)设点Mn(n,
| 1 |
| an |
| k |
| (x-1)2 |
考点:数列与不等式的综合
专题:计算题,证明题,等差数列与等比数列,不等式的解法及应用
分析:(1)由题意得出递推公式,写出即可;(2)用放缩法证明不等式成立,(3)化简,说明是递增数列即可.
解答:
解:(Ⅰ)∵当n≥2时,点Pn是把线段Pn-1Pn+1作n等分的分点中最靠近Pn-1的点,
∴PnPn+1=(n-1)PnPn-1,
即an=(n-1)an-1,
则a2=1,a3=2,a4=6;
(Ⅱ)证明:∵an=(n-1)an-1,
∴
=1,
=2,…,
=(n-1);
∴an=(n-1)!(n≥2),
由于a1=1也符合上式,
则an=(n-1)!
则
+
+…+
=1+1+
+
+…+
<1+1+
+
+…+
=1+
=3-
<3.
(Ⅲ)若点Mn(n,
)(n>2,n∈N*)在函数y=
(k>0)的图象上,
则k=
×(n-1)2=
(n>2,n∈N*),
则在n>2,n∈N*时,k随着n增大而减小,
则不存在两个点同时在函数y=
(k>0)的图象上.
∴PnPn+1=(n-1)PnPn-1,
即an=(n-1)an-1,
则a2=1,a3=2,a4=6;
(Ⅱ)证明:∵an=(n-1)an-1,
∴
| a2 |
| a1 |
| a3 |
| a2 |
| an |
| an-1 |
∴an=(n-1)!(n≥2),
由于a1=1也符合上式,
则an=(n-1)!
则
| 1 |
| a1 |
| 1 |
| a 2 |
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 3! |
| 1 |
| (n-1)! |
<1+1+
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-2 |
=1+
1(1-(
| ||
(1-
|
| 1 |
| 2n-2 |
(Ⅲ)若点Mn(n,
| 1 |
| an |
| k |
| (x-1)2 |
则k=
| 1 |
| an |
| n-1 |
| (n-2)! |
则在n>2,n∈N*时,k随着n增大而减小,
则不存在两个点同时在函数y=
| k |
| (x-1)2 |
点评:本题综合考查了数列与不等式,在数列中注意递推公式的应用及等比数列前n项和公式,在不等式中要注意根据要证明的不等式适当的放缩.属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若x>y>1,0<a<1,那么下列各式中正确的是( )
| A、x-a>y-a |
| B、logax>logay |
| C、ax<ay |
| D、ax>ay |
 已知关于x的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,2),且与x轴交于不同的两点A、B,点A的坐标是(1,0).
已知关于x的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,2),且与x轴交于不同的两点A、B,点A的坐标是(1,0).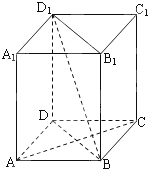 如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,且AB=1,D1D=
如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,且AB=1,D1D=