题目内容
已知方程x2+y2-2(t+3)x+2(1-4t2)y+16t4+9=0表示一个圆.
(1)求t的取值范围;
(2)求圆的圆心和半径;
(3)求该圆的半径r的最大值及此时圆的标准方程.
(1)求t的取值范围;
(2)求圆的圆心和半径;
(3)求该圆的半径r的最大值及此时圆的标准方程.
考点:圆的一般方程
专题:直线与圆
分析:(1)直接利用二元二次方程表示圆的条件,列出不等式即可求出t的取值范围;
(2)利用圆的一般方程,直接求圆的圆心和半径;
(3)化简该圆的半径r的表达式,通过二次函数的最值的求法,求出最大值,即可求解圆的标准方程.
(2)利用圆的一般方程,直接求圆的圆心和半径;
(3)化简该圆的半径r的表达式,通过二次函数的最值的求法,求出最大值,即可求解圆的标准方程.
解答:
解:(1)由圆的一般方程x2+y2-2(t+3)x+2(1-4t2)y+16t4+9=0得:
[-2(t+3)]2+4(1-4t2)2-4 (16t4+9)>0,…(1分)
即:-7t2+6t+1>0,…(2分)
解得:-
<t<1.…(3分)
(2)圆心为:(-
,-
)即圆心为:(t+3,4t2-1)…(4分)
半径r=
=
;…(6分)
(3)r=
=
,…(8分)
所以当t=
时,rmax=
,…(10分)
故圆的标准方程为:(x-
)2+(y+
)2=
.…(12分)
[-2(t+3)]2+4(1-4t2)2-4 (16t4+9)>0,…(1分)
即:-7t2+6t+1>0,…(2分)
解得:-
| 1 |
| 7 |
(2)圆心为:(-
| -2(t+3) |
| 2 |
| 2(1-4t2) |
| 2 |
半径r=
| 1 |
| 2 |
| [-2(t+3)]2+4(1-4t2)2-4(16t4+9) |
| -7t2+6t+1 |
(3)r=
| -7t2+6t+1 |
-7(t-
|
所以当t=
| 3 |
| 7 |
2
| ||
| 7 |
故圆的标准方程为:(x-
| 24 |
| 7 |
| 13 |
| 49 |
| 16 |
| 7 |
点评:本题考查二元二次方程表示圆的充要条件,圆的一般方程的应用,考察计算能力.

练习册系列答案
相关题目
函数f(x)=
的值域( )
|
| A、[-9,+∞) | ||
B、[-9,0]∪(0,
| ||
C、[-9,0]∪[
| ||
D、[-8,0]∪[
|
设a=
dx,则
sinxdx=( )
| ∫ | 2 0 |
| 4-x2 |
| ∫ | a 0 |
| A、2π | B、π | C、2 | D、1 |
已知集合M={x|y=2x},N={x|y=lg(x-1)},则M∩∁RN=( )
| A、(-∞,1] | B、(-∞,1) |
| C、R | D、∅ |
光线从点A(-2,
)射到x轴上的B点后,被x轴反射,这时反射光线恰好过点C(1,2
),则光线BC所在直线的倾斜角为( )
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
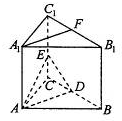 如图,在直三棱柱ABC-A1B1C1中,AB=AC,D、E分别是棱BC、CC1上的点(点D不在BC的端点处),且AD⊥DE,F为B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,D、E分别是棱BC、CC1上的点(点D不在BC的端点处),且AD⊥DE,F为B1C1的中点.