题目内容
某化工厂近期要生产一批化工试剂,经市场调查得知,生产这批试剂厂家的生产成本有以下三个方面:①生产1单位试剂需要原料费50元;②支付所有职工的工资总额由7500元的基本工资和每生产1单位试剂补贴20元组成;③后续保养的平均费用是每单位(x+
-30)元(试剂的总产量为x单位,50≤x≤200).
(Ⅰ)把生产每单位试剂的成本表示为x的函数关系P(x),并求出P(x)的最小值;
(Ⅱ)如果产品全部卖出,据测算销售额Q(x)(元)关于产量x(单位)的函数关系为Q(x)=1240x-
x3,试问:当产量为多少时生产这批试剂的利润最高?
| 600 |
| x |
(Ⅰ)把生产每单位试剂的成本表示为x的函数关系P(x),并求出P(x)的最小值;
(Ⅱ)如果产品全部卖出,据测算销售额Q(x)(元)关于产量x(单位)的函数关系为Q(x)=1240x-
| 1 |
| 30 |
考点:根据实际问题选择函数类型
专题:综合题,导数的综合应用
分析:(Ⅰ)根据生产这批试剂厂家的生产成本有三个方面,可得函数关系P(x),利用配方法求出P(x)的最小值;
(Ⅱ)生产这批试剂的利润L(x)=1240x-
x3-(x2+40x+8100),利用导数,可得结论.
(Ⅱ)生产这批试剂的利润L(x)=1240x-
| 1 |
| 30 |
解答:
解:(Ⅰ)P(x)=[50x+7500+20x+x(x+
-30)]÷x=x+
+40,
∵50≤x≤200,
∴x=90时,P(x)的最小值为220元;
(Ⅱ)生产这批试剂的利润L(x)=1240x-
x3-(x2+40x+8100),
∴L′(x)=1200-
x2-2x=-
(x+120)(x-100),
∴50≤x<100时,L′(x)>0,100<x≤200时,L′(x)<0,
∴x=100时,函数取得极大值,也是最大值,即产量为100单位时生产这批试剂的利润最高.
| 600 |
| x |
| 8100 |
| x |
∵50≤x≤200,
∴x=90时,P(x)的最小值为220元;
(Ⅱ)生产这批试剂的利润L(x)=1240x-
| 1 |
| 30 |
∴L′(x)=1200-
| 1 |
| 10 |
| 1 |
| 10 |
∴50≤x<100时,L′(x)>0,100<x≤200时,L′(x)<0,
∴x=100时,函数取得极大值,也是最大值,即产量为100单位时生产这批试剂的利润最高.
点评:本题考查根据实际问题选择函数类型,考查配方法,考查导数知识的综合运用,属于中档题.

练习册系列答案
相关题目
设a=
dx,则
sinxdx=( )
| ∫ | 2 0 |
| 4-x2 |
| ∫ | a 0 |
| A、2π | B、π | C、2 | D、1 |
已知数列{an},定直线l:(m+3)x-(2m+4)y-m-9=0,若(n,an)在直线l上,则数列{an}的前13项和为( )
| A、10 | B、21 | C、39 | D、78 |
已知集合M={x|y=2x},N={x|y=lg(x-1)},则M∩∁RN=( )
| A、(-∞,1] | B、(-∞,1) |
| C、R | D、∅ |
光线从点A(-2,
)射到x轴上的B点后,被x轴反射,这时反射光线恰好过点C(1,2
),则光线BC所在直线的倾斜角为( )
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
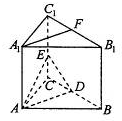 如图,在直三棱柱ABC-A1B1C1中,AB=AC,D、E分别是棱BC、CC1上的点(点D不在BC的端点处),且AD⊥DE,F为B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,D、E分别是棱BC、CC1上的点(点D不在BC的端点处),且AD⊥DE,F为B1C1的中点.