题目内容
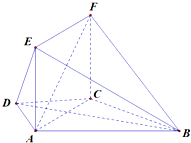 如图,在梯形ABCD中,AD⊥CD,AD∥CD,AD=CD=
如图,在梯形ABCD中,AD⊥CD,AD∥CD,AD=CD=| 1 |
| 2 |
(1)求证:AF⊥BC;
(2)求二面角B-AF-C的余弦值.
考点:与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明FC⊥BC,BC⊥AC,可得BC⊥平面ACFE,即可证明AF⊥BC;
(2)过C作CG⊥AF于G点,连BG,则∠BGC为所求角,求出tan∠BGC=
,可求二面角B-AF-C的余弦值.
(2)过C作CG⊥AF于G点,连BG,则∠BGC为所求角,求出tan∠BGC=
| 3 |
解答:
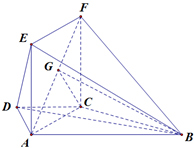 (1)证明:∵平面ACFE⊥平面ABCD,四边形ACFE是矩形,
(1)证明:∵平面ACFE⊥平面ABCD,四边形ACFE是矩形,
∴FC⊥平面ABCD,
∴FC⊥BC,
∵AD⊥CD,AD∥CD,AD=CD=
AB=a,
∴BC⊥AC,
∵FC∩AC=C,
∴BC⊥平面ACFE,
∴AF⊥BC;
(2)解:过C作CG⊥AF于G点,连BG
又AF⊥BC,故AF⊥平面BCG,于是∠BGC为所求角.
在△BGC中,BC=
a,CG=
=
a,
于是tan∠BGC=
,∴cos∠BGC=
.
 (1)证明:∵平面ACFE⊥平面ABCD,四边形ACFE是矩形,
(1)证明:∵平面ACFE⊥平面ABCD,四边形ACFE是矩形,∴FC⊥平面ABCD,
∴FC⊥BC,
∵AD⊥CD,AD∥CD,AD=CD=
| 1 |
| 2 |
∴BC⊥AC,
∵FC∩AC=C,
∴BC⊥平面ACFE,
∴AF⊥BC;
(2)解:过C作CG⊥AF于G点,连BG
又AF⊥BC,故AF⊥平面BCG,于是∠BGC为所求角.
在△BGC中,BC=
| 2 |
| AC•CF |
| AF |
| ||
| 3 |
于是tan∠BGC=
| 3 |
| 1 |
| 2 |
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
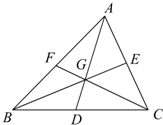 在△ABC中,AD,BE,CF分别是BC,CA,AB边上的中线,G是它们的交点,则下列等式中不正确的是( )
在△ABC中,AD,BE,CF分别是BC,CA,AB边上的中线,G是它们的交点,则下列等式中不正确的是( )A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
函数f(x)=lgx+x-3的零点所在的区间是( )
| A、(1,2) |
| B、(3,4) |
| C、(2,3) |
| D、(0,1) |
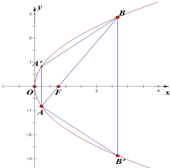 在平面直角坐标系xOy中,抛物线y2=2px上一点到焦点F的距离与到y轴的距离的差为1.
在平面直角坐标系xOy中,抛物线y2=2px上一点到焦点F的距离与到y轴的距离的差为1. 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA=AB=1,AD=
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA=AB=1,AD=