题目内容
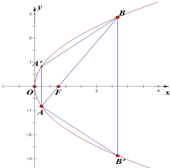 在平面直角坐标系xOy中,抛物线y2=2px上一点到焦点F的距离与到y轴的距离的差为1.
在平面直角坐标系xOy中,抛物线y2=2px上一点到焦点F的距离与到y轴的距离的差为1.(1)求抛物线的方程;
(2)过F作直线交抛物线于A,B两点,且A,B关于x轴的对称点分别为A′,B′,四边形AA′BB′的面积为S,求
| S |
| |AB|2 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线中的最值与范围问题
分析:(1)由题意知
=1;
(2)设A(
,y1),B(
,y2),直线AB的方程为x=ky+1.由梯形面积公式及弦长公式可表示
,由
,得y2-4ky-4=0,y1+y2=4k,代入韦达定理得
为k的函数,利用基本不等式可求其最大值;
| p |
| 2 |
(2)设A(
| y12 |
| 4 |
| y22 |
| 4 |
| S |
| |AB|2 |
|
| S |
| |AB|2 |
解答:
解:(1)由题意知
=1,∴p=2,
∴抛物线方程为:y2=4x.
(2)设A(
,y1),B(
,y2),直线AB的方程为x=ky+1.
于是S=
|2y1-2y2|•|
-
|=
(y1-y2)2|y1+y2|,
|AB|=
|y1-y2|,于是
=
•
,
又由
,得y2-4ky-4=0,y1+y2=4k,
于是
=
•
=
=
≤
,当且仅当k=±1时,等号成立.
∴
的最大值为
,此时直线AB的斜率也为±1.
| p |
| 2 |
∴抛物线方程为:y2=4x.
(2)设A(
| y12 |
| 4 |
| y22 |
| 4 |
于是S=
| 1 |
| 2 |
| y12 |
| 4 |
| y22 |
| 4 |
| 1 |
| 4 |
|AB|=
| 1+k2 |
| S |
| |AB|2 |
| 1 |
| 4 |
| |y1+y2| |
| 1+k2 |
又由
|
于是
| S |
| |AB|2 |
| 1 |
| 4 |
| |y1+y2| |
| 1+k2 |
| |k| |
| 1+k2 |
| 1 | ||
|k|+
|
| 1 |
| 2 |
∴
| S |
| |AB|2 |
| 1 |
| 2 |
点评:该题考查抛物线的方程、性质,考查直线与抛物线的位置关系,考查方程思想,弦长公式、韦达定理是该类问题常用知识,要熟练掌握.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
函数f(x)的定义域为R,f(2)=4,对?x∈R,f′(x)>3,则f(x)>3x-2的解集是( )
| A、(-∞,+∞) |
| B、(2,+∞) |
| C、(-∞,2) |
| D、(-2,2) |
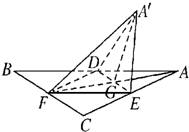 如图,等边三角形ABC的中线AF与中位线DE相交于G,已知△A′ED是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,等边三角形ABC的中线AF与中位线DE相交于G,已知△A′ED是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A、动点A′在平面ABC上的射影在线段AF上 |
| B、恒有平面A′GF⊥平面ACDE |
| C、三棱锥′-EFD的体积有最大值 |
| D、异面直线A′E与BD不可能垂直 |
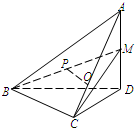 如图在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2
如图在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2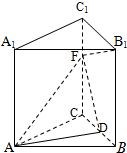 在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是C1C上一点,且CF=2a.
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是C1C上一点,且CF=2a.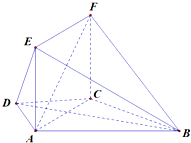 如图,在梯形ABCD中,AD⊥CD,AD∥CD,AD=CD=
如图,在梯形ABCD中,AD⊥CD,AD∥CD,AD=CD=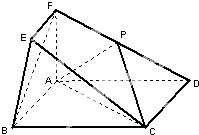 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.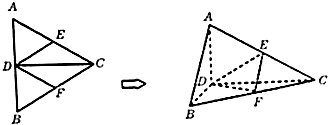
 如图,在⊙O的直径AB的延长线上任取一点C,过点C引直线与⊙O交于点D、E,在⊙O上再取一点F,使
如图,在⊙O的直径AB的延长线上任取一点C,过点C引直线与⊙O交于点D、E,在⊙O上再取一点F,使